تماس با ما
گروه تلگرام ما
هشدارهای ما
آمار و اطلاعات
پروژه
دانلود فیلم آموزش بازسازی داده های اقلیمی ناقص و مفقود شده باران، دما، چاه و... در اکسل
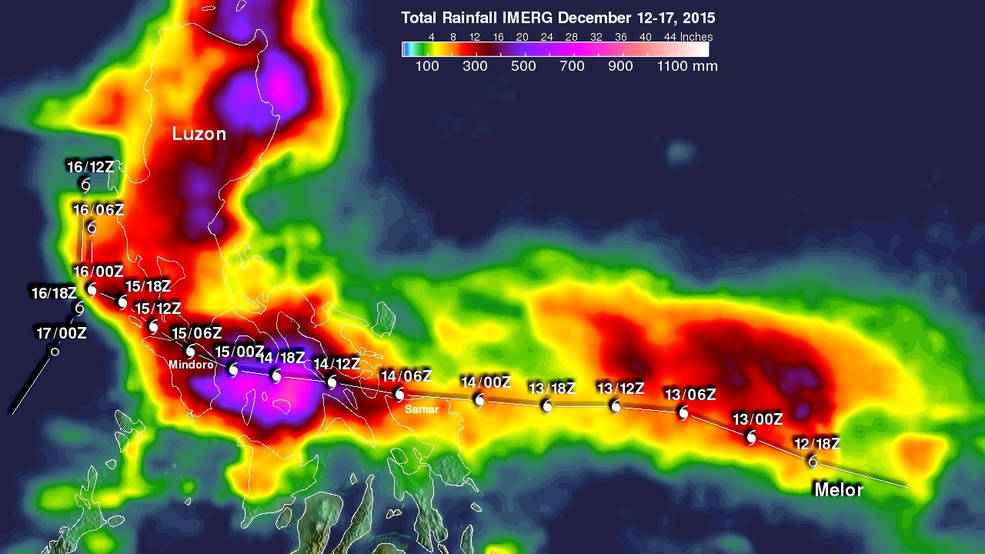
بازسازی داده های اقلیمی و زمینی به سبب وجود مقادیر ناقص یکی از مهم ترین گام های پیش پردازش در این اطالاعات می باشد. در واقع می توان گفت داده های محیطی نظیر داده های بارش، دما، سیل و حتی داده هایی نظیر مقادیر سطح آب زیرزمینی در چاه های مشاهده ای و پیزومترها؛ به سبب و علل گوناگونی که می توانند در دسته های مشخص دسته بندی گردند همواره دارای مقادیری ناقص می باشند. نقص داده گاهی سبب متوقف شدن کل محاسبات گسترده ای در یک مدل سازی می شود؛ به نحوی که تا تکمیل این نواقص امکان عبور به گام وجود ندارد. در بسیاری موارد نیز لازم است ایستگاه های مختلف در یک بازه زمانی به تعداد متناسب و متناظر دارای داده باشند، به نحوی که امکان انجام آزمون های آماری همگنی و روند یابی و کفایت داده همچون ماکوس و... ممکن گردد. در این میان راه های گوناگونی برای ترمیم و تصحیح این مجموعه ها پیشنهاد شده است. که می توان به موارد ذیل اشاره کرد:
1- روش درون یابی و برون یابی
ساده ترین روش برای تخمین داده های مفقود شده آن است که چند نقطه دیگر را که دارای آمار می باشند در اطراف نقطه مورد نظر انتخاب می کنیم و با توجه به فاصله ای که دارند، خطوط تراز آن منطقه را ترسیم کرده و سپس مشاهده نماییم که چه خطی از نقطه مود نظر عبور می کند. برای مثال اگر آمار باران سال 1360 در ایستگاه A مفقود باشد، از روی آمار ایستگاه های مجاور و با توجه به درون یابی بین داده های موجود می توان خطوط هم باران سال 1360 را ترسیم نموده و سپس مقدار مجهول را استخراج نمود. یکی از دلائل ترسیم خطوط هم دما نیز همین امر می باشد. این گفته نیازمند توضیحات گسترده روش های میان یابی و اصول آماری آن است که شما می توانید ویدئوی آموزشی با همین موضوع را در اینجا ببینید.
2- روش تفاضل ها و نسبت ها
فرض کنید آمار بارندگی ایستگاه A از سال 1355 تا 1365 در اختیار است و می خواهیم آمار مفقود آن را برای سال های 1350 تا 1354 و سال 1359 تخمین بزنیم. یک ایستگاه که آمار آن کامل و مورد اطمینان است را در همان منطقه به عنوان مبنا انتخاب کرده، و فرض کنید ایستگاه B در این منطقه به همین عنوان در ستون سوم انتخاب شده باشد. مقایسه این دو ایستگاه نشان می دهد که در سال های 1355 تا 1358 و 1360 تا 1365 هر دو ایستگاه دارای آمار می باشند. چانچه:
در آن Xb= میانگین بارندگی در سال های مشترک آماری (سال هایی که هر دو ایستگاه دارای آمار هستند) برای ایستگاه مبنا.
و Xa= میانگین بارندگی در سال های مشترک آماری برای ایستگاه A باشد، مقدار بارندگی برای هر یک از سال های فاقد آمار در ایستگاه A به شرح ذیل محاسبه می شود:
با تقسیم میانگین بارش در سال های مشترک آماری در A بر همین مقدار در ایستگاه B و سپس ضرب این حاصل در مقدار میانگین کل ایستگاه B میانگین کل در ایستگاه A را خواهیم داشت (جواب 272).
3- روش میانگین گیری
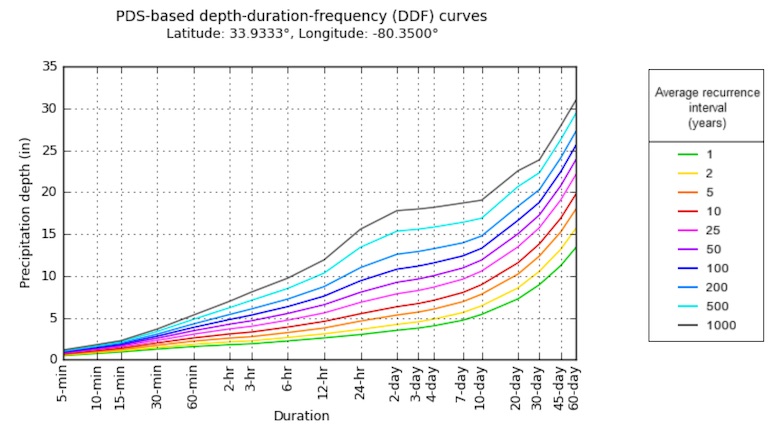
این روش بیشتر برای تخمین بارندگی به کار می رود. فرض می شود که در ایستگاه X آمار بارندگی در یک روز یا در یک سال معین مفقود باشد. سه ایستگاه 1 و 2 و 3 در مجاورت آن در نظر می گیریم. اگر N1 و N2 و N3 و Nx به ترتیب متوسط بارندگی در ایستگاه های مذکور باشد. و P1 و P2 و P3 و Px نیز به ترتیب مقادیر آمار بارندگی (در یک مدت مشخص) در ایستگاه های مذکور باشد، چنان چه اختلاف N1 و N2 و N3 و Nx کمتر از 10% از Nx باشد، در این صورت برای بدست آوردن Px از فرمول ذیل استفاده می شود (روش میانگین گیری ریاضی):
ولی اگر مقدار اختلاف N1 و N2 و N3 و Nx بیش از 10% اختلاف Nx باشد فرمول زیر مورد استفاده دارد (روش نسبت نرمال):
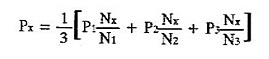
4- روش نموداری
یکی دیگر از روش های معمول برای اصلاح داده های مشکوک یا تخمین داده برای نقطه ای که به کل فاقد آمار هیدرولوژی و یا هواشناسی است روش به اصطلاح گرافیکی می باشد. معمولا اگر بخواهیم بارندگی را برای یک نقطه تخمین بزنیم روی یک نقشه که از محل هدف در اختیار داریم چند ایستگاه دیگر که آماری تکمیل دارند (در همان زمان مورد نظر) انتخاب می کنیم؛ از نقطه ای که فاقد آمار است دو محور عمود بر هم رسم می نماییم. مثلا ایستگاه های A و B و C و D و E را انتخاب کرده و از نقطه مجهول O که آمار آن در اختیار نیست، دو محور متعامد ترسم می کنیم. سپس قدر مطلق مختصات هر نقطه را نسبت به این محورها اندازه گیری می کنیم. با داشتن بارندگی در هر یک از نقاط و مختصات آنها جدولی مشابه با آنچه در ادامه آمده است تشکیل و بارش را تخمین خواهیم زد.
برای دریافت ویدئوی آموزشی بازسازی داده های آماری کلیک کنید.
شناسه تلگرام مدیر سایت: SubBasin@
نشانی ایمیل: behzadsarhadi@gmail.com
(سوالات تخصصی را در گروه تلگرام ارسال کنید)
_______________________________________________________
در منابع آب
نظرات (۰)