دوره بازگشت به برآورد احتمال روی‌دادن یک پدیده طبیعی مثل سیل یا تغییرات دبی رودخانه گفته می‌شود. معمولاً محاسبه و برآورد دوره بازگشت بر پایه اندازه‌گیری آماری داده‌های تاریخی به منظور دست‌یابی به میانگین زمان تکرار پدیده در یک دوره زمانی است و برای تحلیل خطر بروز یک پدیده مورد استفاده قرار می‌گیرد. شامل تصمیم گیری در مورد اینکه آیا اجازه می دهد پروژه در منطقه ای از ریسک خاص پیش برود یا طراحی ساختارها برای مقاومت در برابر حوادث با یک دوره بازگشت خاص، مجاز است. تجزیه و تحلیل زیر فرض می کند که احتمال وقوع این رویداد به مرور تغییر نمی کند و مستقل از وقایع گذشته است.

دوره بازگشت به عنوان مفهوم متقابل بسامد مورد انتظار

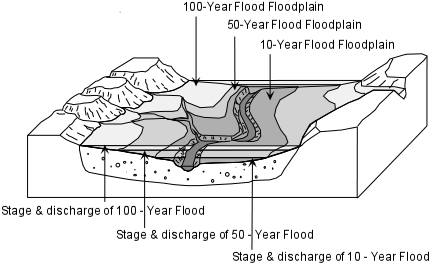
دوره بازگشت نظری بین وقایع، معکوس بسامد متوسط ​​وقوع است. به عنوان مثال، یک سیل 10 ساله دارای احتمال 1/10 = 0.1 یا 10٪ احتمال وقوع در هر سال است و یک سیل 50 ساله دارای 0.02 یا 2٪ احتمال وقوع در هر سال است.

این بدان معنا نیست که یک سیل 100 ساله مرتباً در هر 100 سال یا فقط یک بار در 100 سال اتفاق می افتد. با وجود تعبیرات نام "دوره بازگشت"، در هر دوره 100 ساله معین، یک رویداد 100 ساله ممکن است یک بار، دو بار، بیشتر یا اصلاً اتفاق نیفتد و هر نتیجه یک احتمال دارد که می تواند مانند مطالب زیر محاسبه شود. اما برای یک دوره چند هزار ساله به طور متوسط با همین احتمال به وقوع می پیوندد.

همچنین، دوره بازگشت برآورد شده زیر یک مقدار آماری است: از مجموعه ای از داده ها (مشاهدات) محاسبه می شود، همانطور که از ارزش نظری در توزیع ایده آل متمایز است. در واقع کسی نمی داند که بزرگی خاص یا بیشتر با احتمال 1٪ اتفاق می افتد، فقط این که دقیقاً یکبار در 100 سال مشاهده شده است.

این تمایز بسیار مهم است زیرا مشاهدات کمی در مورد اتفاقات نادر وجود دارد: به عنوان مثال اگر مشاهدات به 400 سال برمی گردد، شدیدترین رویداد (یک رویداد 400 ساله با تعریف آماری) ممکن است بعداً با مشاهده طولانی تر، به عنوان 200 ساله طبقه بندی شود. رویداد سال (در صورت وقوع یک رویداد قابل مقایسه بلافاصله) یا یک رویداد 500 ساله (در صورت عدم وجود یک رویداد قابل مقایسه برای 100 سال دیگر) خواهد بود. به همین علت است که گفته می شود طول دوره آماری برای محاسبات باید به اندازه کافی بزرگ باشد.

علاوه بر این، نمی توان اندازه یک رویداد 1000 ساله را بر اساس چنین سوابق مشخص کرد بلکه باید در یک مدل آماری از پیش بینی میزان چنین رویدادی (غیرحضوری) استفاده کند. حتی اگر بازه بازگشت تاریخی بسیار کمتر از 1000 سال باشد، اگر تعدادی از رویدادهای کمتر با ماهیت مشابه ثبت شده باشد، استفاده از چنین مدلی احتمالاً اطلاعات مفیدی را برای کمک به برآورد فاصله بازده آینده ارائه می دهد.

تخمین دوره بازگشت

برای وقوع سیل ممکن است این رویداد از نظر متر مکعب در ثانیه یا ارتفاع اندازه گیری شود. از نظر طوفان، از نظر ارتفاع موج بالا، و به طور مشابه برای سایر رویدادها. این فرمول Weibull است که محاسبه را به شکل زیر بدست خواهد داد:

توزیع احتمال

کارشناسان علاقه دارند که بتواند دوره بازگشت را در مدل های احتمالی تفسیر کنند. منطقی ترین تفسیر برای این امر، دوره بازگشت به عنوان نرخ شمارش در توزیع پواسون است. زیرا ارزش انتظار نرخ وقایع است. یک تعبیر جایگزین این است که احتمال آن برای حالت سالانه برنولی در توزیع دوجمله ای بررسی شود. این البته متناسب برآورد تعیین نمی شود زیرا هر سال حالت مستقل برنولی را نشان نمی دهد بلکه یک زمان مستقل است. این مساله عمدتاً آکادمیک است زیرا نتایج به دست آمده در تفسیرهای پواسون و دو جمله ای مشابه خواهند بود.

توزیع پواسون

تابع زیر معادله احتمال توزیع  پواسون است.

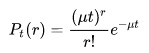
جایی که r تعداد وقایعی است که احتمال برای آن محاسبه می شود، t زمان مورد نظر و   نرخ شمارش است.

مثال

اگر مدت زمان بازگشت 234 سال باشد () ، پس احتمال عدم وقوع در 10 سال به صورت زیر است:

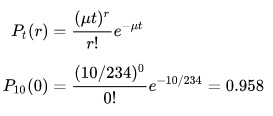
توزیع دو جمله ای

در یک دوره معین از n سال، احتمال تعداد معینی از وقایع مربوط به دوره بازگشت  توسط توزیع دوجمله ای به شرح زیر داده شده است.

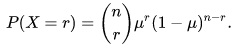
این تنها در صورتی معتبر است که احتمال بیش از یک مورد در سال صفر باشد. غالباً این یک تقریب نزدیک است، در این صورت احتمالات حاصل از این فرمول تقریباً معادل نگه می دارند.

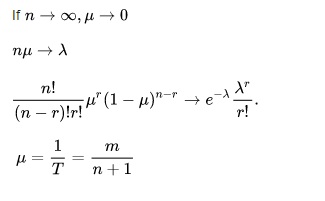
جایی که:

T بازه بازگشت است

n تعداد سال های دارای داده است.

m تعداد وقایع ثبت شده از رویداد مورد نظر است

مثال

با توجه به اینکه دوره بازگشت یک رویداد 100 ساله است، 

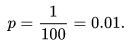
بنابراین احتمال وقوع چنین رویدادی دقیقاً یکبار در 10 سال پی در پی وجود دارد:

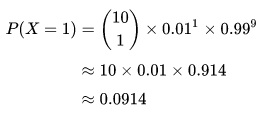
تحلیل ریسک

دوره برگشت برای تجزیه و تحلیل ریسک مفید است (مانند خطر طبیعی، ذاتی یا هیدرولوژیکی از شکست). هنگام پرداختن به انتظارات طراحی سازه، دوره بازگشت در محاسبه ریسک سازه مفید است. احتمال حداقل یک رویداد که بیش از حد طراحی در طول عمر مورد انتظار سازه باشد، تکمیل احتمال وقوع بیانگر این است که هیچ رویدادی وجود نخواهد داشت که از محدوده طراحی فراتر رود.

معادله زیر ارزیابی این پارامتر است:

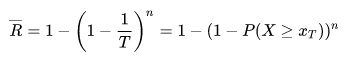
جایی که 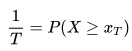 عبارتی است برای احتمال وقوع رویداد مورد نظر در یک سال

n عمر مورد انتظار ساختار است.

مفهوم و نحوه محاسبه دوره بازگشت سیل - بخش اول

ورود به بخش پروژه جامع هیدرولوژی

مدیر سایت: بهزاد سرهادی

شماره تلفن: 09190622992

شناسه تلگرام مدیر سایت: SubBasin@

نشانی ایمیل: behzadsarhadi@gmail.com

(سوالات تخصصی را در گروه تلگرام ارسال کنید)

_______________________________________________________

پروژه تخصصی در لینکدین

×

 براي پيوستن به بزرگترين گروه تلگرام علوم و مهندسي آب با امکان تبادل نظر بين اعضاء کليک کنيد

کتاب کاربرد مدل QUAL2KW

کتاب کاربرد GIS در منابع آب

کتاب محاسبه سيل طرح