تماس با ما
گروه تلگرام ما
هشدارهای ما
آمار و اطلاعات
پروژه
نمونه مثال تجزیه و تحلیل داده های بارش
مختصات چهار ایستگاه سنجش بارش (A = (3،4) ،B = (9،4) ،C = (3،12 و (D = (912 است. مقدار بارش مشاهده شده در این سنج ها به ترتیب PA = 15 میلی متر، PB = 23 میلی متر، PC = 10 میلی متر، PD = 19 میلی متر است. این ایستگاه ها در یک حوضه مستطیل شکل قرار دارند که مرزهای آنها توسط مختصات (0،0)، (14،0)، (14،16)، (0،16) تعریف شده است. میانگین بارش در این حوضه را با استفاده از روش چند ضلعی Thiessen و روش میانگین حسابی محاسبه کنید.
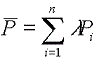
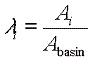
با استفاده از چند ضلعی های Thiessen، مناطق نفوذ AA = 48؛ AB = 64؛ AC = 48؛ AD = 64 است. مساحت حوضه Abasin = 224 است. بنابراین متوسط میانگین بارش به صورت زیر بدست می آید:
MAP = (48/224)15 + (64/224)23 + (48/224)10 + (64/224)19 = 17.36 mm
Arithmetic Average method: MAP = (15 + 23 + 10 + 19)/4 = 16.75 mm
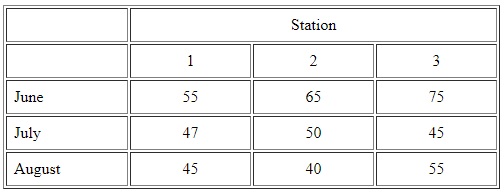
2. مقدار بارش برای ماه های ژوئن، ژوئیه و آگوست از سابقه یک ایستگاه سنج در یک حوضه مفقود است. این ایستگاه به شبکه چهارتایی در آن حوضه تعلق دارد. برای این سه ماه، سه ایستگاه دیگر موارد زیر را ثبت کردند:
اگر بارش متوسط بلند مدت سالانه در چهار ایستگاه برابر:
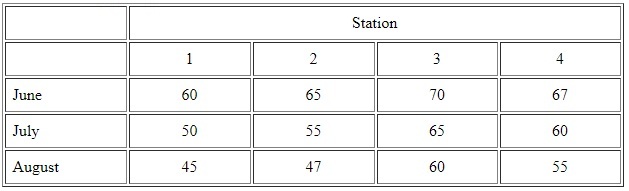
از روش نسبت عادی استفاده کنید،
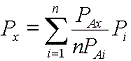
June: Px = ((67/60)55+(67/65)65+(67/70)75)/3 = 66.73
July: Px = ((60/50)47+(60/55)50+(60/65)45)/3 = 50.83
August: Px = ((55/45)45+(55/47)40+(55/60)55)/3 = 50.74
3. فرض کنید یک واقعه بارشی با شدت 1.25 سانتی متر در ساعت بر فراز یک حوضه یکنواخت جنگلی منطقه 20 کیلومتر مربع سقوط می کند. اگر تنها تلفات آب در این رویداد به دلیل رهگیری است، میزان آب موجود در حوضه را به عنوان رواناب طوفان به مدت 1 ساعت و 2 ساعت بارندگی را محاسبه کنید. حجم رهگیری به عنوان تابعی از میزان بارندگی P داده می شود،
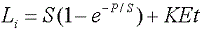
فرض کنید K برابر 1.5 و S برابر 0.2 سانتی متر و میزان تبخیر صفر است.
محاسبه کل حجم بارش:
P = (1.25 cm/h) (1 h) = 1.25 cm
P = (1.25 cm/h) (2 h) = 2.5 cm
برای به دست آوردن از معادله 4 استفاده کنید:
Li = (0.2 cm) (1 - exp(-1.25/0.2)) = 0.1996 cm
Li = (0.2 cm) (1 - exp(-2.5/0.2)) = 0.2 cm
با فرض اینکه تغییری در ذخیره حوضه ایجاد نشود، خروجی حوضه برابر است با:
Volume of Output = (P - Li)*Abasin = ((1.25 cm - 0.1996 cm)/100 cm/m ) (20 106 m2) = 210,080.0 m3
Volume of Output = (P - Li)*Abasin = ((2.50 cm - 0.2 cm)/100 cm/m ) (20 106 m2) = 460,000.0 m3
4- مسئله 3 را تکرار کنید اما با فرض اینکه علاوه بر رهگیری ، به دلیل ذخیره افسردگی ضررهایی نیز به همراه دارد. معادله ذخیره سازی افسردگی عبارت است از:
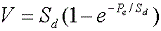
فرض کنید Sd برابر 0.2 سانتی متر است. نسبت رواناب برای این شرایط چیست؟ میزان رواناب چقدر می توانست در نیمه راه طوفان تولید شود؟
Pe = P - Li = 1.0504 cm. Thus, V = (0.2 cm) (1 - exp(-1.0504/0.2)) = 0.1989 cm
Pe = P - Li = 2.3 cm. Thus, V = (0.2 cm) (1 - exp(-2.3/0.2)) = 0.2 cm
باز هم با فرض اینکه تغییری در ذخیره حوضه ایجاد نشده باشد، خروجی حوضه برابر است با:
Volume of Output = (Pe - V)*Abasin = ((1.0504 cm - 0.1989 cm)/100 cm/m ) (20 106 m2) = 170,300.0 m3
Volume of Output = (Pe - V)*Abasin = ((2.30 cm - 0.2 cm)/100 cm/m ) (20 106 m2) = 420,000.0 m3
شناسه تلگرام مدیر سایت: SubBasin@
نشانی ایمیل: behzadsarhadi@gmail.com
(سوالات تخصصی را در گروه تلگرام ارسال کنید)
_______________________________________________________
در منابع آب
نظرات (۰)