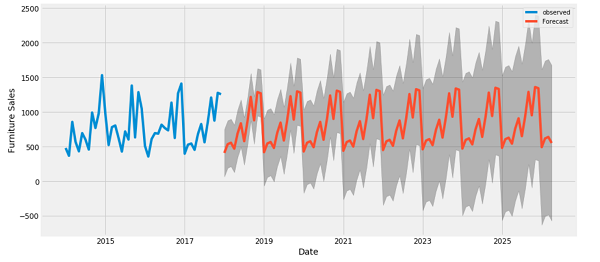
مدل های تک مرحله ای

ساده ترین مدلی که می توانید بر اساس این نوع داده ها بسازید، مدلی است که مقدار یک ویژگی را تنها در شرایط فعلی، 1 برابر گام (1 ساعت) در آینده پیش بینی می کند. بنابراین با ایجاد مدل هایی برای پیش بینی مقدار یک ساعت (T (degC در آینده شروع کنید.

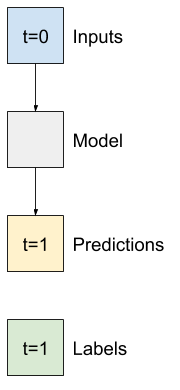
یک شی WindowGenerator را برای تولید این جفت های تک مرحله ای (input, label) پیکربندی کنید:

single_step_window = WindowGenerator(
    input_width=1, label_width=1, shift=1,
    label_columns=['T (degC)'])
single_step_window

Total window size: 2
Input indices: [0]
Label indices: [1]
Label column name(s): ['T (degC)']

شی window پنجره مجموعه های tf.data.Datasets را از مجموعه های آموزش، اعتبار سنجی و آزمایش ایجاد می کند، به شما امکان می دهد به راحتی در دسته های داده تکرار کنید.

for example_inputs, example_labels in single_step_window.train.take(1):
  print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
  print(f'Labels shape (batch, time, features): {example_labels.shape}')

Inputs shape (batch, time, features): (32, 1, 19)
Labels shape (batch, time, features): (32, 1, 1)

پایه (Baseline)

قبل از ساخت یک مدل قابل آموزش خوب است که یک پایه عملکرد به عنوان یک نقطه برای مقایسه با مدلهای پیچیده بعدی داشته باشید.

این اولین کار پیش بینی دمای 1 ساعت در آینده با توجه به مقدار فعلی همه ویژگی ها است. مقادیر فعلی شامل دمای فعلی است.

بنابراین با مدلی شروع کنید که فقط دمای فعلی را به عنوان پیش بینی برگرداند و "بدون تغییر" را پیش بینی کند. این یک پایه اساسی است زیرا دما به آرامی تغییر می کند. مطمئناً، اگر در آینده پیش بینی کنید، این خط پایه کمتر کار خواهد کرد.

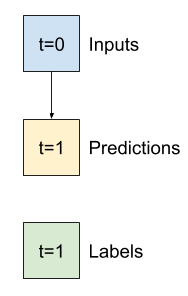
class Baseline(tf.keras.Model):
  def __init__(self, label_index=None):
    super().__init__()
    self.label_index = label_index

  def call(self, inputs):
    if self.label_index is None:
      return inputs
    result = inputs[:, :, self.label_index]
    return result[:, :, tf.newaxis]

این مدل را نمونه برداری و ارزیابی کنید:

baseline = Baseline(label_index=column_indices['T (degC)'])

baseline.compile(loss=tf.losses.MeanSquaredError(),
                 metrics=[tf.metrics.MeanAbsoluteError()])

val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(single_step_window.val)
performance['Baseline'] = baseline.evaluate(single_step_window.test, verbose=0)

439/439 [==============================] - 1s 2ms/step - loss: 0.0129 - mean_absolute_error: 0.0787

برخی از معیارهای عملکرد را چاپ کرده است، اما این احساسات را در مورد عملکرد خوب مدل به شما نمی دهد.

WindowGenerator یک روش طرح دارد، اما طرح ها فقط با یک نمونه جالب نخواهند بود. بنابراین، یک WindowGenerator گسترده تر ایجاد کنید که همزمان ویندوزهای 24 ساعته ورودی و برچسب تولید کند.

wide_window نحوه عملکرد مدل را تغییر نمی دهد. این مدل بر اساس یک گام زمان ورودی واحد، هنوز پیش بینی های 1 ساعته ای را برای آینده ارائه می دهد. در اینجا محور زمان مانند محور دسته عمل می کند: هر پیش بینی به طور مستقل و بدون تعامل بین مراحل زمانی انجام می شود.

wide_window = WindowGenerator(
    input_width=24, label_width=24, shift=1,
    label_columns=['T (degC)'])

wide_window

Total window size: 25
Input indices: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
Label indices: [ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24]
Label column name(s): ['T (degC)']

این پنجره توسعه یافته می تواند مستقیماً به همان مدل پایه بدون هیچگونه تغییر کد منتقل شود. این امکان وجود دارد زیرا ورودی ها و برچسب ها تعداد زمان های یکسانی دارند و خط پایه ورودی را به خروجی هدایت می کند:

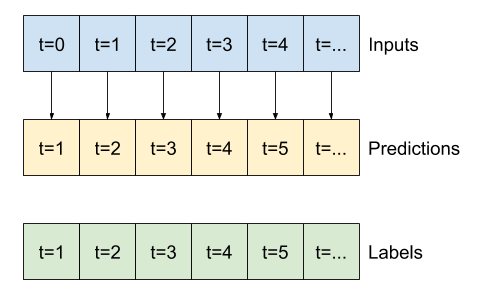
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)

Input shape: (32, 24, 19)
Output shape: (32, 24, 1)

با رسم پیش بینی های مدل پایه می توانید ببینید که این مدل ها به سادگی برچسب ها هستند و 1 ساعت به سمت راست منتقل می شوند.

wide_window.plot(baseline)

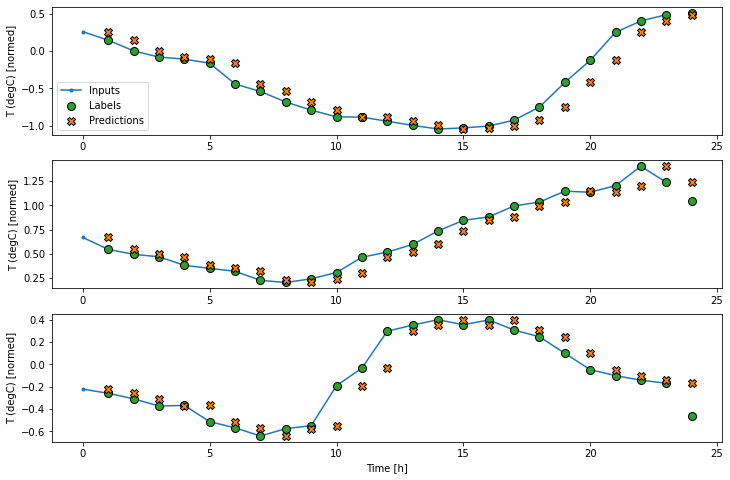
در نمودارهای فوق سه نمونه، مدل تک مرحله ای در طول 24 ساعت اجرا می شود. این سزاوار توضیح است:

• خط آبی "ورودی" دمای ورودی را در هر مرحله نشان می دهد. مدل تمام ویژگی ها را بازیابی می کند ، این نمودار فقط دما را نشان می دهد.
• نقاط سبز "Labels" مقدار پیش بینی هدف را نشان می دهد. این نقاط در زمان پیش بینی نشان داده می شوند نه در زمان ورود. به همین دلیل دامنه برچسب ها نسبت به ورودی ها 1 مرحله تغییر مکان می یابد.
• ضربدرهای نارنجی "پیش بینی ها" پیش بینی مدل برای هر مرحله زمان خروجی است. اگر مدل کاملاً پیش بینی می کرد ، پیش بینی ها مستقیماً روی "برچسب ها" قرار می گرفتند.

مدل خطی (Linear model)

ساده ترین مدل قابل آموزش که می توانید برای این کار اعمال کنید، قرار دادن تحول خطی بین ورودی و خروجی است. در این حالت خروجی از یک مرحله زمانی فقط به آن مرحله بستگی دارد:

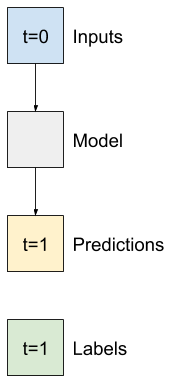
یک layers.Dense و بدون مجموعه فعال یک مدل خطی است. این لایه فقط آخرین محور داده را از batch, time, inputs) به (batch, time, units) تبدیل می کند، و به طور مستقل برای هر مورد در محورهای دسته و زمان اعمال می شود.

linear = tf.keras.Sequential([
    tf.keras.layers.Dense(units=1)
])

print('Input shape:', single_step_window.example[0].shape)
print('Output shape:', linear(single_step_window.example[0]).shape)

Input shape: (32, 1, 19)
Output shape: (32, 1, 1)

این آموزش بسیاری از مدل ها را آموزش می دهد، بنابراین روش آموزش را به صورت تابعی بسته بندی کنید:

MAX_EPOCHS = 20

def compile_and_fit(model, window, patience=2):
  early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss',
                                                    patience=patience,
                                                    mode='min')

  model.compile(loss=tf.losses.MeanSquaredError(),
                optimizer=tf.optimizers.Adam(),
                metrics=[tf.metrics.MeanAbsoluteError()])

  history = model.fit(window.train, epochs=MAX_EPOCHS,
                      validation_data=window.val,
                      callbacks=[early_stopping])
  return history

مدل را آموزش دهید و عملکرد آن را ارزیابی کنید:

history = compile_and_fit(linear, single_step_window)

val_performance['Linear'] = linear.evaluate(single_step_window.val)
performance['Linear'] = linear.evaluate(single_step_window.test, verbose=0)

Epoch 1/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.2064 - mean_absolute_error: 0.2944 - val_loss: 0.0101 - val_mean_absolute_error: 0.0752
Epoch 2/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0099 - mean_absolute_error: 0.0734 - val_loss: 0.0089 - val_mean_absolute_error: 0.0708
Epoch 3/20
1534/1534 [==============================] - 5s 3ms/step - loss: 0.0091 - mean_absolute_error: 0.0700 - val_loss: 0.0088 - val_mean_absolute_error: 0.0702
Epoch 4/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0091 - mean_absolute_error: 0.0699 - val_loss: 0.0088 - val_mean_absolute_error: 0.0703
Epoch 5/20
1534/1534 [==============================] - 6s 4ms/step - loss: 0.0091 - mean_absolute_error: 0.0699 - val_loss: 0.0088 - val_mean_absolute_error: 0.0707
439/439 [==============================] - 1s 2ms/step - loss: 0.0088 - mean_absolute_error: 0.0707

مانند مدل baseline، مدل خطی را می توان در دسته پنجره های عریض فراخوانی کرد. با استفاده از این روش مدل مجموعه ای از پیش بینی های مستقل را در مراحل زمانی متوالی انجام می دهد. محور time مانند یک محور batch دیگر عمل می کند. در هر مرحله زمانی هیچ تعاملی بین پیش بینی ها وجود ندارد.

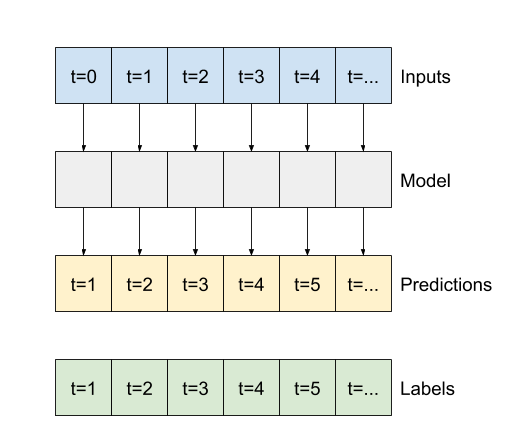
print('Input shape:', wide_window.example[0].shape)
print('Output shape:', baseline(wide_window.example[0]).shape)

در اینجا نمودار پیش بینی های مثال آن در windows_window آورده شده است، توجه داشته باشید که چگونه در بسیاری از موارد پیش بینی به وضوح بهتر از بازگشت دمای ورودی است، اما در چند مورد بدتر است:

wide_window.plot(linear)

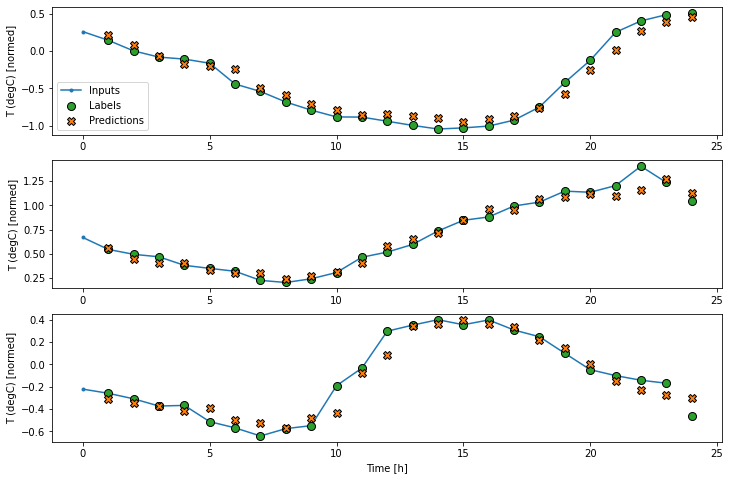
یک مزیت مدل های خطی این است که تفسیر آنها نسبتاً ساده است. می توانید وزن های لایه را بیرون بکشید و وزن اختصاص داده شده به هر ورودی را ببینید:

plt.bar(x = range(len(train_df.columns)),
        height=linear.layers[0].kernel[:,0].numpy())
axis = plt.gca()
axis.set_xticks(range(len(train_df.columns)))
_ = axis.set_xticklabels(train_df.columns, rotation=90)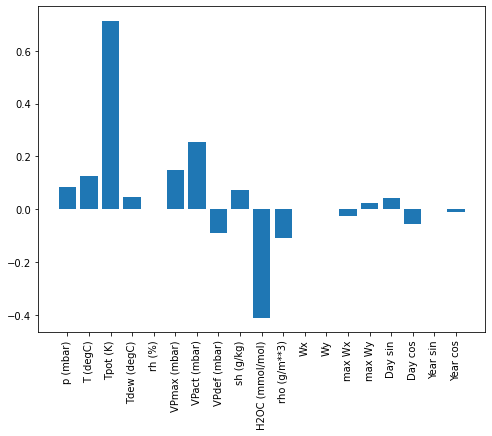

گاهی اوقات مدل حتی بیشترین وزن را روی ورودی (T (degC نمی گذارد. این یکی از خطرات مقداردهی اولیه است.

تراکم (Dense)

قبل از استفاده از مدل هایی که در واقع در چند مرحله زمانی کار می کنند، ارزش بررسی عملکرد مدل های عمیق تر، قدرتمندتر و تک مرحله ورودی را دارد. در اینجا یک مدل شبیه به مدل linear وجود دارد، با این تفاوت که چندین لایه Dense بین ورودی و خروجی را جمع می کند:

dense = tf.keras.Sequential([
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=1)
])

history = compile_and_fit(dense, single_step_window)

val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)

Epoch 1/20
1534/1534 [==============================] - 7s 4ms/step - loss: 0.0701 - mean_absolute_error: 0.1282 - val_loss: 0.0090 - val_mean_absolute_error: 0.0719
Epoch 2/20
1534/1534 [==============================] - 7s 4ms/step - loss: 0.0081 - mean_absolute_error: 0.0653 - val_loss: 0.0069 - val_mean_absolute_error: 0.0592
Epoch 3/20
1534/1534 [==============================] - 7s 4ms/step - loss: 0.0075 - mean_absolute_error: 0.0621 - val_loss: 0.0069 - val_mean_absolute_error: 0.0607
Epoch 4/20
1534/1534 [==============================] - 7s 4ms/step - loss: 0.0073 - mean_absolute_error: 0.0610 - val_loss: 0.0067 - val_mean_absolute_error: 0.0590
Epoch 5/20
1534/1534 [==============================] - 7s 4ms/step - loss: 0.0070 - mean_absolute_error: 0.0597 - val_loss: 0.0065 - val_mean_absolute_error: 0.0571
Epoch 6/20
1534/1534 [==============================] - 7s 4ms/step - loss: 0.0069 - mean_absolute_error: 0.0593 - val_loss: 0.0067 - val_mean_absolute_error: 0.0590
Epoch 7/20
1534/1534 [==============================] - 7s 4ms/step - loss: 0.0069 - mean_absolute_error: 0.0592 - val_loss: 0.0064 - val_mean_absolute_error: 0.0564
Epoch 8/20
1534/1534 [==============================] - 7s 5ms/step - loss: 0.0069 - mean_absolute_error: 0.0588 - val_loss: 0.0074 - val_mean_absolute_error: 0.0628
Epoch 9/20
1534/1534 [==============================] - 7s 4ms/step - loss: 0.0067 - mean_absolute_error: 0.0580 - val_loss: 0.0067 - val_mean_absolute_error: 0.0587
439/439 [==============================] - 1s 3ms/step - loss: 0.0067 - mean_absolute_error: 0.0587

تراکم چند مرحله ای (Multi-step dense)

مدل تک مرحله ای هیچ زمینه ای برای مقادیر فعلی ورودی های خود ندارد. نمی تواند ببیند که ویژگی های ورودی با گذشت زمان چگونه تغییر می کنند. برای رسیدگی به این مسئله، مدل هنگام پیش بینی نیاز به دسترسی به مراحل زمانی متعدد دارد:

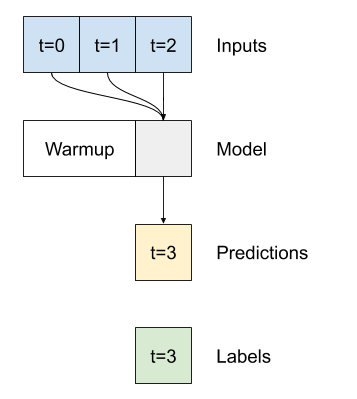
مدل های baseline ،linear و dense هر مرحله به طور مستقل انجام می شوند. در اینجا مدل چندین مرحله زمانی را به عنوان ورودی برای تولید یک خروجی واحد برمی دارد.

یک WindowGenerator ایجاد کنید که دسته هایی از 3 ساعت ورودی و 1 ساعت برچسب ها را تولید کند:

توجه داشته باشید که پارامتر Window's shift نسبت به انتهای دو پنجره است.

CONV_WIDTH = 3
conv_window = WindowGenerator(
    input_width=CONV_WIDTH,
    label_width=1,
    shift=1,
    label_columns=['T (degC)'])

conv_window

Total window size: 4
Input indices: [0 1 2]
Label indices: [3]
Label column name(s): ['T (degC)']

conv_window.plot()
plt.title("Given 3h as input, predict 1h into the future.")

Text(0.5, 1.0, 'Given 3h as input, predict 1h into the future.')

با افزودن یک لایه می توانید یک مدل dense را روی پنجره چند مرحله ای آموزش دهید.  layers.Flatten زا به عنوان اولین لایه مدل اضافه کنید:

multi_step_dense = tf.keras.Sequential([
    # Shape: (time, features) => (time*features)
    tf.keras.layers.Flatten(),
    tf.keras.layers.Dense(units=32, activation='relu'),
    tf.keras.layers.Dense(units=32, activation='relu'),
    tf.keras.layers.Dense(units=1),
    # Add back the time dimension.
    # Shape: (outputs) => (1, outputs)
    tf.keras.layers.Reshape([1, -1]),
])

print('Input shape:', conv_window.example[0].shape)
print('Output shape:', multi_step_dense(conv_window.example[0]).shape)

Input shape: (32, 3, 19)
Output shape: (32, 1, 1)

history = compile_and_fit(multi_step_dense, conv_window)

IPython.display.clear_output()
val_performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.val)
performance['Multi step dense'] = multi_step_dense.evaluate(conv_window.test, verbose=0)

438/438 [==============================] - 1s 2ms/step - loss: 0.0062 - mean_absolute_error: 0.0559

conv_window.plot(multi_step_dense)

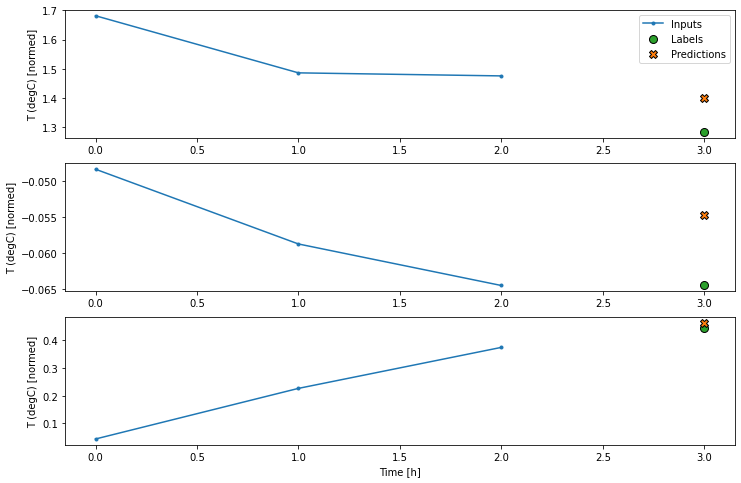
نکته اصلی اصلی این رویکرد این است که مدل حاصل فقط روی پنجره های ورودی دقیقاً به این شکل قابل اجرا است.

print('Input shape:', wide_window.example[0].shape)
try:
  print('Output shape:', multi_step_dense(wide_window.example[0]).shape)
except Exception as e:
  print(f'\n{type(e).__name__}:{e}')

Input shape: (32, 24, 19)

ValueError:Input 0 of layer dense_4 is incompatible with the layer: expected axis -1 of input shape to have value 57 but received input with shape (32, 456)

مدل های کانولوشن در بخش بعدی این مشکل را برطرف می کنند.

شبکه عصبی کانولوشن

یک لایه کانولوشن (layers.Conv1D) نیز چندین مرحله زمان را به عنوان ورودی برای هر پیش بینی انجام می دهد.

در زیر same مدل multi_step_dense وجود دارد که با یک کانولوشن دوباره نوشته شده است.

به تغییرات توجه داشته باشید:

layers.Flatten و اولین layers.Denseبا layers.Conv1D جایگزین می شود.

layers.Reshape دیگر لازم نیست زیرا کانولوشن محور زمان را در خروجی خود نگه می دارد.

conv_model = tf.keras.Sequential([
    tf.keras.layers.Conv1D(filters=32,
                           kernel_size=(CONV_WIDTH,),
                           activation='relu'),
    tf.keras.layers.Dense(units=32, activation='relu'),
    tf.keras.layers.Dense(units=1),
])

آن را روی یک نمونه دسته ای اجرا کنید تا ببینید که مدل خروجی هایی با شکل مورد انتظار تولید می کند:

print("Conv model on `conv_window`")
print('Input shape:', conv_window.example[0].shape)
print('Output shape:', conv_model(conv_window.example[0]).shape)

Conv model on `conv_window`
Input shape: (32, 3, 19)
Output shape: (32, 1, 1)

آن را در conv_window آموزش داده و ارزیابی کنید و باید عملکردی مشابه مدل چند مرحله ای داشته باشد.

history = compile_and_fit(conv_model, conv_window)

IPython.display.clear_output()
val_performance['Conv'] = conv_model.evaluate(conv_window.val)
performance['Conv'] = conv_model.evaluate(conv_window.test, verbose=0)

تفاوتی که بین این مدل conv_model و مدل multi_step_dense وجود دارد این است که مدل conv_model را می توان بر روی ورودی های هر طول اجرا کرد. لایه کانولوشن به پنجره کشویی ورودی اعمال می شود:

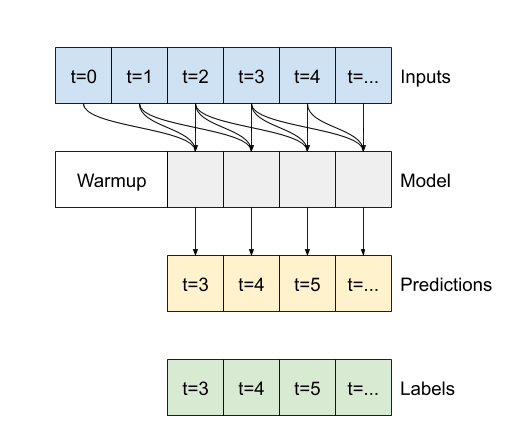
اگر آن را روی ورودی وسیع تری اجرا کنید، خروجی گسترده تری تولید می کند:

print("Wide window")
print('Input shape:', wide_window.example[0].shape)
print('Labels shape:', wide_window.example[1].shape)
print('Output shape:', conv_model(wide_window.example[0]).shape)

Wide window
Input shape: (32, 24, 19)
Labels shape: (32, 24, 1)
Output shape: (32, 22, 1)

توجه داشته باشید که خروجی کوتاهتر از ورودی است. برای اینکه کار آموزش یا نقشه کشی انجام شود، باید برچسب ها و پیش بینی به همان طول داشته باشید. بنابراین برای تولید پنجره های گسترده با چند مرحله زمان ورودی اضافی، یک WindowGenerator بسازید تا طول برچسب و پیش بینی مطابقت داشته باشد:

LABEL_WIDTH = 24
INPUT_WIDTH = LABEL_WIDTH + (CONV_WIDTH - 1)
wide_conv_window = WindowGenerator(
    input_width=INPUT_WIDTH,
    label_width=LABEL_WIDTH,
    shift=1,
    label_columns=['T (degC)'])

wide_conv_window

Total window size: 27
Input indices: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
 24 25]
Label indices: [ 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26]
Label column name(s): ['T (degC)']

print("Wide conv window")
print('Input shape:', wide_conv_window.example[0].shape)
print('Labels shape:', wide_conv_window.example[1].shape)
print('Output shape:', conv_model(wide_conv_window.example[0]).shape)

Wide conv window
Input shape: (32, 26, 19)
Labels shape: (32, 24, 1)
Output shape: (32, 24, 1)

اکنون می توانید پیش بینی های مدل را در پنجره وسیع تری ترسیم کنید. قبل از اولین پیش بینی به 3 مرحله زمان ورودی توجه داشته باشید. هر پیش بینی در اینجا بر اساس 3 مرحله قبل است:

wide_conv_window.plot(conv_model)

شبکه عصبی بازگشتی

شبکه عصبی بازگشتی (RNN) نوعی شبکه عصبی است که برای داده های سری زمانی مناسب است. RNN یک سری زمانی را مرحله به مرحله پردازش می کند و یک حالت داخلی را از زمان به مرحله به مرحله دیگر حفظ می کند.

برای جزئیات بیشتر، آموزش تولید متن یا راهنمای RNN را مطالعه کنید.

در این آموزش، شما از یک لایه RNN به نام Long Short Memory (LSTM) استفاده خواهید کرد.

یک آرگومان سازنده مهم برای تمام لایه های keras RNN آرگومان return_sequences است. این تنظیم می تواند لایه را به یکی از دو روش پیکربندی کند.

اگر False باشد، پیش فرض، لایه فقط خروجی گام آخر را برمی گرداند، و به مدل زمان می دهد تا حالت داخلی خود را گرم کند قبل از اینکه یک پیش بینی انجام دهد:

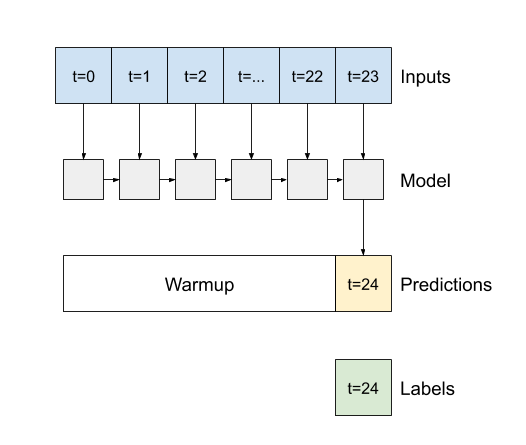
اگر True باشد، لایه برای هر ورودی یک خروجی برمی گرداند. این برای موارد زیر مفید است:

• قرار دادن لایه های RNN.
• آموزش یک مدل در چند زمان به طور همزمان.

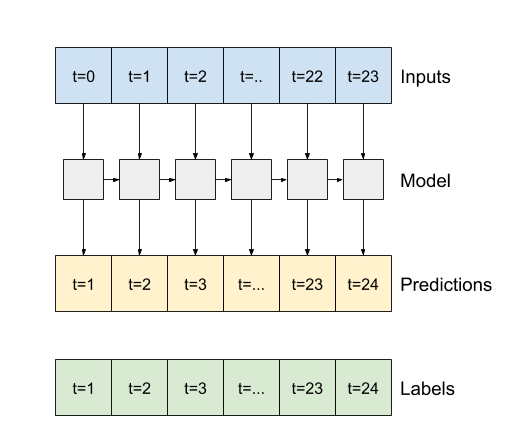
lstm_model = tf.keras.models.Sequential([
    # Shape [batch, time, features] => [batch, time, lstm_units]
    tf.keras.layers.LSTM(32, return_sequences=True),
    # Shape => [batch, time, features]
    tf.keras.layers.Dense(units=1)
])

زمانی که return_sequences=True مدل می تواند همزمان با 24 ساعت داده آموزش ببیند.

توجه: این یک دید بدبینانه از عملکرد مدل ارائه می دهد. در اولین گام بار مدل به مراحل قبلی دسترسی ندارد و بنابراین نمی تواند نتیجه ای بهتر از مدل های خطی و متراکم ساده نشان دهد.

print('Input shape:', wide_window.example[0].shape)
print('Output shape:', lstm_model(wide_window.example[0]).shape)

Input shape: (32, 24, 19)
Output shape: (32, 24, 1)

history = compile_and_fit(lstm_model, wide_window)

IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate(wide_window.val)
performance['LSTM'] = lstm_model.evaluate(wide_window.test, verbose=0)

438/438 [==============================] - 2s 4ms/step - loss: 0.0055 - mean_absolute_error: 0.0509

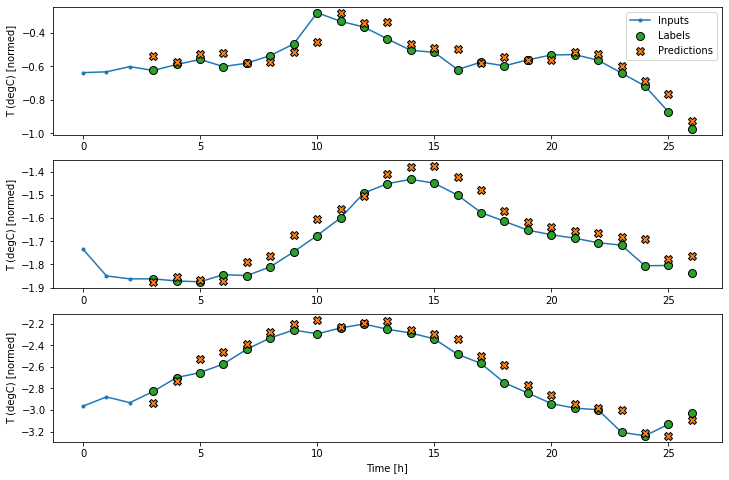
wide_window.plot(lstm_model)

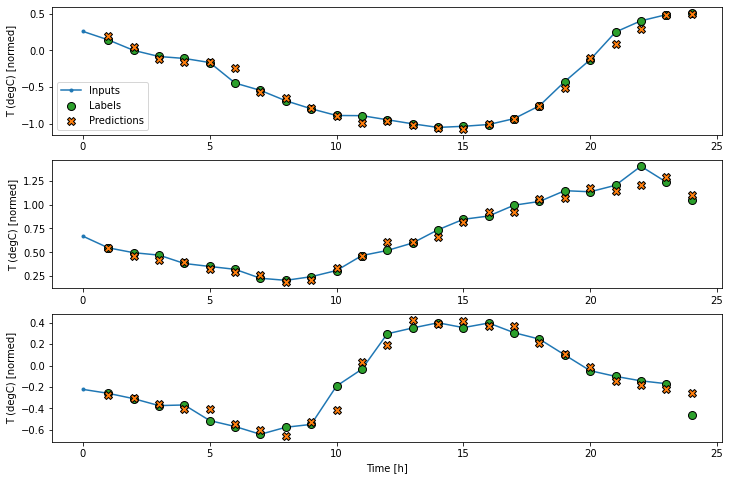
کارایی مدل

با استفاده از این مجموعه داده به طور معمول هر یک از مدل ها کمی بهتر از مدل قبلی خود عمل می کنند.

x = np.arange(len(performance))
width = 0.3
metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]

plt.ylabel('mean_absolute_error [T (degC), normalized]')
plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
           rotation=45)
_ = plt.legend()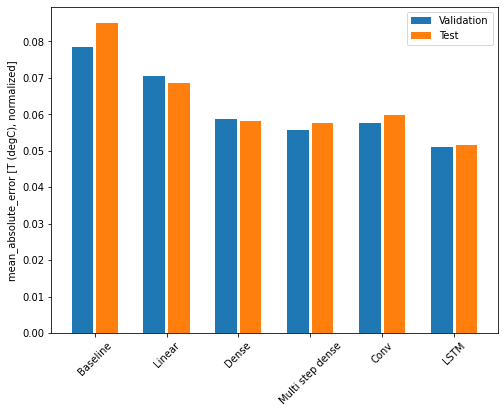

for name, value in performance.items():
  print(f'{name:12s}: {value[1]:0.4f}')

Baseline    : 0.0852
Linear      : 0.0686
Dense       : 0.0581
Multi step dense: 0.0577
Conv        : 0.0598
LSTM        : 0.0516

مدل های چند خروجی

مدل ها تاکنون همه یک ویژگی خروجی واحد، T (degC) را برای یک گام واحد پیش بینی کرده اند.

همه این مدل ها را می توان فقط با تغییر تعداد واحد در لایه خروجی و تنظیم پنجره های آموزش برای درج تمام ویژگی ها در labels، به چندین ویژگی پیش بینی کرد.

single_step_window = WindowGenerator(
    # `WindowGenerator` returns all features as labels if you 
    # don't set the `label_columns` argument.
    input_width=1, label_width=1, shift=1)

wide_window = WindowGenerator(
    input_width=24, label_width=24, shift=1)

for example_inputs, example_labels in wide_window.train.take(1):
  print(f'Inputs shape (batch, time, features): {example_inputs.shape}')
  print(f'Labels shape (batch, time, features): {example_labels.shape}')

Inputs shape (batch, time, features): (32, 24, 19)
Labels shape (batch, time, features): (32, 24, 19

در بالا توجه داشته باشید که محور features برچسب ها اکنون به جای 1، دارای عمق ورودی هستند.

پایه (Baseline)

در اینجا می توان از همان مدل پایه استفاده کرد، اما این بار به جای انتخاب یک label_index خاص، همه ویژگی ها را تکرار می کند.

baseline = Baseline()
baseline.compile(loss=tf.losses.MeanSquaredError(),
                 metrics=[tf.metrics.MeanAbsoluteError()])

val_performance = {}
performance = {}
val_performance['Baseline'] = baseline.evaluate(wide_window.val)
performance['Baseline'] = baseline.evaluate(wide_window.test, verbose=0)

438/438 [==============================] - 1s 2ms/step - loss: 0.0883 - mean_absolute_error: 0.1589

تراکم (Dense)

dense = tf.keras.Sequential([
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=64, activation='relu'),
    tf.keras.layers.Dense(units=num_features)
])

history = compile_and_fit(dense, single_step_window)

IPython.display.clear_output()
val_performance['Dense'] = dense.evaluate(single_step_window.val)
performance['Dense'] = dense.evaluate(single_step_window.test, verbose=0)

439/439 [==============================] - 2s 3ms/step - loss: 0.0687 - mean_absolute_error: 0.1342

RNN

%%time
wide_window = WindowGenerator(
    input_width=24, label_width=24, shift=1)

lstm_model = tf.keras.models.Sequential([
    # Shape [batch, time, features] => [batch, time, lstm_units]
    tf.keras.layers.LSTM(32, return_sequences=True),
    # Shape => [batch, time, features]
    tf.keras.layers.Dense(units=num_features)
])

history = compile_and_fit(lstm_model, wide_window)

IPython.display.clear_output()
val_performance['LSTM'] = lstm_model.evaluate( wide_window.val)
performance['LSTM'] = lstm_model.evaluate( wide_window.test, verbose=0)

print()

438/438 [==============================] - 2s 4ms/step - loss: 0.0614 - mean_absolute_error: 0.1198

CPU times: user 6min 10s, sys: 1min 25s, total: 7min 35s
Wall time: 2min 55s

پیشرفته: اتصالات باقیمانده

مدل Baseline از اوایل این واقعیت استفاده کرد که توالی از مرحله به مرحله تغییر نمی کند. هر مدلی که تاکنون در این آموزش آموزش دیده بود به طور تصادفی اولیه سازی می شد و سپس باید می فهمید که خروجی نسبت به مرحله زمان قبلی یک تغییر کوچک است.

اگرچه می توانید با مقداردهی Baseline دقیق از پس این مسئله برآیید، ساخت آن در ساختار مدل ساده تر است.

در تجزیه و تحلیل سری های زمانی معمول است که مدل هایی ساخته شوند که به جای پیش بینی مقدار بعدی، پیش بینی کنند که مقدار در مرحله بعدی چگونه تغییر می کند. به طور مشابه، "شبکه های باقیمانده" یا "ResNets" در یادگیری عمیق به معماری هایی اشاره دارند که هر لایه به نتیجه جمع شده مدل می افزاید.

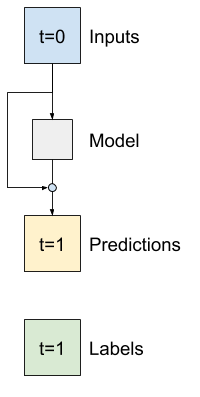
اینگونه است که شما از دانش کوچک بودن تغییر استفاده می کنید.

اساساً این مدل را برای مطابقت با خط مبنا Baseline می کند. برای این کار به مدل ها کمک می کند تا با عملکرد کمی بهتر، سریعتر همگرا شوند.

این روش می تواند همراه با هر مدلی که در این مقاله آموزش داده شده استفاده شود.

در اینجا از مدل LSTM استفاده می شود، به استفاده از tf.initializers.zeros توجه داشته باشید تا اطمینان حاصل کنید که تغییرات اولیه پیش بینی شده اندک هستند و بر اتصال باقیمانده غلبه نمی کنند. در اینجا شیب هایی برای شکست تقارن وجود ندارد، زیرا صفرها فقط روی لایه آخر استفاده می شوند.

class ResidualWrapper(tf.keras.Model):
  def __init__(self, model):
    super().__init__()
    self.model = model

  def call(self, inputs, *args, **kwargs):
    delta = self.model(inputs, *args, **kwargs)

    # The prediction for each timestep is the input
    # from the previous time step plus the delta
    # calculated by the model.
    return inputs + delta

%%time
residual_lstm = ResidualWrapper(
    tf.keras.Sequential([
    tf.keras.layers.LSTM(32, return_sequences=True),
    tf.keras.layers.Dense(
        num_features,
        # The predicted deltas should start small
        # So initialize the output layer with zeros
        kernel_initializer=tf.initializers.zeros)
]))

history = compile_and_fit(residual_lstm, wide_window)

IPython.display.clear_output()
val_performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.val)
performance['Residual LSTM'] = residual_lstm.evaluate(wide_window.test, verbose=0)
print()

438/438 [==============================] - 1s 3ms/step - loss: 0.0623 - mean_absolute_error: 0.1180

CPU times: user 2min 25s, sys: 34.6 s, total: 3min
Wall time: 1min 7s

کارایی

در اینجا عملکرد کلی این مدلهای چند خروجی آورده شده است.

x = np.arange(len(performance))
width = 0.3

metric_name = 'mean_absolute_error'
metric_index = lstm_model.metrics_names.index('mean_absolute_error')
val_mae = [v[metric_index] for v in val_performance.values()]
test_mae = [v[metric_index] for v in performance.values()]

plt.bar(x - 0.17, val_mae, width, label='Validation')
plt.bar(x + 0.17, test_mae, width, label='Test')
plt.xticks(ticks=x, labels=performance.keys(),
           rotation=45)
plt.ylabel('MAE (average over all outputs)')
_ = plt.legend()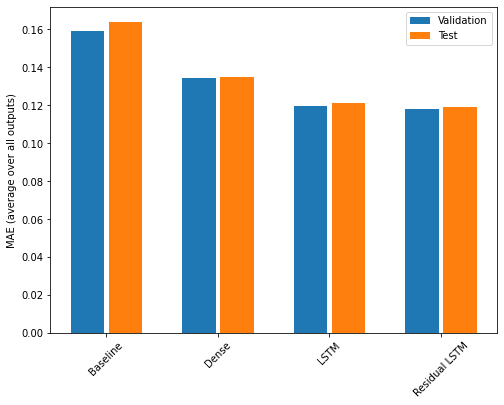

عملکردهای فوق در تمام خروجی های مدل به طور متوسط ​​است.

for name, value in performance.items():
  print(f'{name:15s}: {value[1]:0.4f}')

Baseline       : 0.1638
Dense          : 0.1349
LSTM           : 0.1214
Residual LSTM  : 0.1192

مدیر سایت: بهزاد سرهادی

شماره تلفن: 09190622992

شناسه تلگرام مدیر سایت: SubBasin@

نشانی ایمیل: behzadsarhadi@gmail.com

(سوالات تخصصی را در گروه تلگرام ارسال کنید)

_______________________________________________________

پروژه تخصصی در لینکدین

×

 براي پيوستن به بزرگترين گروه تلگرام علوم و مهندسي آب با امکان تبادل نظر بين اعضاء کليک کنيد

کتاب کاربرد مدل QUAL2KW

کتاب کاربرد GIS در منابع آب

کتاب محاسبه سيل طرح