6.6 حل عددی مدل موج حرکتی

فرم اول از مدل موج حرکتی برای نشان دادن یک طرح خطی صریح بر روی یک سلول با اختلاف محدود استفاده شده است همانطور که در شکل 4.6 نشان داده شده است.

برای تقریب مشتق فضا از یک تفاضل محدود رو به عقب استفاده می شود، در حالی که مشتق زمان معمولاً در همان موقعیت مکانی  x_j+1 بیان می شود. برای بدست آوردن یک طرح خطی، اصطلاح غیر اشتقاق αβQ^β-1 باید برای یک مقدار Q شناخته شده ارزیابی شود، که در اینجا به عنوان میانگین بین دو مقدار مورب Q_jⁱ⁺¹ و Qⁱ_j+1 پذیرفته می شود.

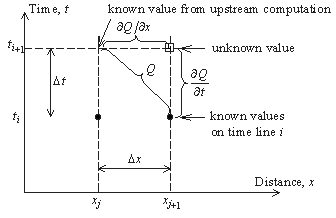
شکل 4.6 سلول تفاضل محدود برای راه حل موج حرکتی خطی.

در نتیجه، فرم تفاضل محدود معادله به شرح زیر است:

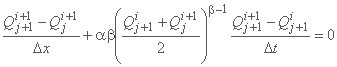
و نتایج ناشناخته Q_j+1ⁱ⁺¹ به شرح زیر است:

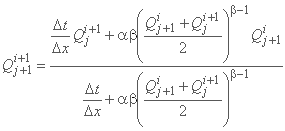
با شروع مقدار هیدروگراف ورودی Q در سطح زمانی t_i+1، محاسبه به ترتیب از بالادست به سمت نقاط شبکه پایین دست، در امتداد خط زمان فعلی  i+1 پیش می رود.

با این حال، این طرح فرض می کند که در ضریب α، محیط P مرطوب ثابت بماند. از طرف دیگر، با استفاده از Q به جای A در مشتق زمان ∂A/∂t، خطاهای محاسباتی نسبی کاهش می یابد. در واقع، با استفاده از لگاریتم معادله حاضر،

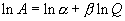
و تمایز، یکی بدست می آورد:

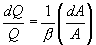
جایی که β برای معادله منینگ 0.6 است. اگر از سطح مقطع A به عنوان متغیر وابسته استفاده شود، خطای تخمین در Q با 1/0.6 ≈ 1.67 بزرگ می شود.

شکل متفاوتی از مدل موج حرکتی خطی به دلیل Cunge (1969) و به نام روش Muskingum-Cunge است. سلول با اختلاف محدود برای این طرح در شکل 5.6 نشان داده شده است.

شکل 5.6 سلول با تفاضل محدود برای روش Muskingum-Cunge.

معادله موج حرکتی:

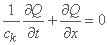
با یک معادله اختلاف محدود در اطراف یک نقطه گسسته به عنوان P در صفحه x-t جایگزین می شود. این نقطه در میانه راه بین خطوط زمان i امین و (i+1) امین قرار دارد و با گام فضایی Δx با ضریب وزنی θ (0 ≤ θ ≤ 1) از مرکز خارج می شود.

فرم تفاضل محدود معادله در اینجا به صورت زیر ظاهر می شود:

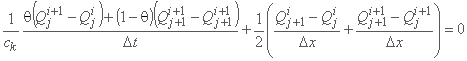
با تفاضل محدود رو به عقب برای مشتق فضا، به طور متوسط ​​بین سطوح زمان، و با تفاضل محدود برای مشتق زمان به طور متوسط ​​بین موقعیت های فضا.

با مرتب سازی مجدد معادله مذکور برای حل 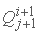، یکی بدست می آید:

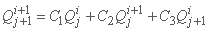
که در آن ضرایب C_i هستند:

;;

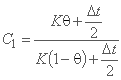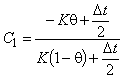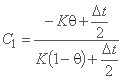
و K = Δx/c_k، مجموع این ضرایب برابر با واحد است.

با مقایسه معادلات با مدل هیدرولوژیکی ماسکینگام (به بخش 5 مراجعه کنید)، یک شباهت رسمی با وجود مبانی نظری مختلف ممکن است مشخص شود.

Cunge نشان داد که وقتی K و θ به طور ثابت در نظر گرفته شوند، معادله حاضر یک حل تقریبی از مدل موج حرکتی است، در حالی که اگر

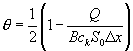 and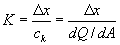 

جایی که ck با Q و B مطابقت دارد، پس معادله 44/6 را می توان یک راه حل تقریبی از موج انتشار برای یک کانال با ثابت S0 در نظر گرفت. وی همچنین نشان داد که برای ثبات عددی لازم است :

0<θ<0,5

مرحله زمانی Δt باید به عنوان Δt ≤ K انتخاب شود.

یک طرح ساده و غیر خطی موج حرکتی از مدل با یک ورودی جانبی q ≠ 0، یک فرم را به عنوان رابطه مذکور برای معادله تفاضل محدود ایجاد می کند اما دارای (c_k)^m به جای c_k  و 1/2(q_jⁱ⁺¹+q_jⁱ) به عنوان سمت راست. در اینجا q_j مربوط به مرحله فضایی Δx است، و  ^m(c_k) توسط:

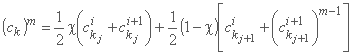 and  (0 ≤ χ ≤ 1)

جایی که:

 m یک تکرار است

 χ ضریب وزن

 c_k با معادله از نظر Q داده شده است

سپس 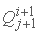 ناشناخته در مرحله تکرار m-th بدست می آید:

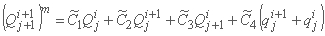
جایی که:

; ;

; 

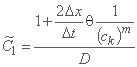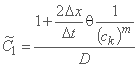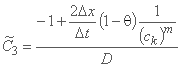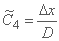
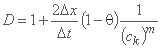
روند تکرار را می توان با مقدار زیر شروع کرد

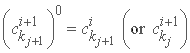
و به عنوان یک معیار همگرایی دنبال می شود، به عنوان مثال:

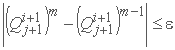
برآورده شده است معیار خطا در مقدار کمی مناسب انتخاب می شود.