3.7 طبقه بندی مدلهای ریاضی

در عملکرد معیارها، طبقه بندی زیر از نتایج مدلهای ریاضی در نظر گرفته شده است:

الف) از نظر تکامل سیستم، مدل ها عبارتند از:

• در رژیم ثابت (حالت پایدار در هیدرولیک)؛
• در رژیم پویا (حالت ناپایدار در هیدرولیک).

به طور کلی، سیستم ها از نظر زمانی تکامل یافته و دارای ویژگی پویایی هستند. با این حال، شرایطی وجود دارد که می توان از مدل های ثابت استفاده کرد (که متغیرهای ورودی، حالت های سیستم و متغیرهای خروجی ثابت هستند و از نظر زمانی متغیر نیستند).

بیایید برای مثال یک سفره آب زیرزمینی را در نظر بگیریم که قرار است ورودی و خروجی آن ثابت باشد (متوسط ​​نفوذ چند ساله، به ترتیب مقادیر چند ساله آب استخراج شده از طریق کارخانه های آب). مدل ثابت به شما امکان می دهد تا پتانسیل هیدرولیکی سفره آب زیرزمینی را تعیین کنید. ملاحظات مشابه ممکن است با اشاره به حرکت دائمی در بسترهای طبیعی آب، کانالها یا لوله ها باشد.

مدل ثابت اجازه می دهد، بنابراین تعیین شرایط تعادل سیستم، که قرار است پایدار باشد، برای ورودی های ثابت.

درصورتی که متغیرها به زمان بستگی داشته باشند، مدل پویا است. ورودی متغیر، خروجی متغیر و همچنین تکامل حالتهای سیستم را تعیین می کند. متغیرها مسیرها، پیوندهای بین متغیرها رابط بین مسیرها را توصیف می کنند.

به طور کلی، مطالعه پویایی سیستم در جهت گذشته و آینده تحقق می یابد، اگرچه در اصل بررسی از حال (یا آینده) به سمت گذشته نیز امکان پذیر است.

ب) با توجه به ماهیت ریاضی روابط مورد استفاده در فرمول بندی مدل، مدل های زیر برجسته می شوند:

• مدل های خطی؛
• مدل های غیر خطی.

مدل زمانی خطی است که متغیرها در اولین قدرت قرار داشته باشند و در حالت خلاف غیر خطی باشند (حداقل یک رابطه شامل یک متغیر در درجه متفاوت از یک باشد).

در بیشتر موارد (و به خصوص برای سیستم های طبیعی)، رابطه بین علت و معلول غیر خطی است. با این حال، برای مطالعات عملی، روابط خطی بین متغیرها تا حد زیادی پذیرفته می شود، به دلیل مزایای استفاده از اصل برهم نهی اثرات. این اصل بر اساس دو فرضیه زیر است:

خروجی سیستم با شدت ورودی متناسب است (ویژگی تناسب).

در مورد یک ورودی پیچیده، که ممکن است در ورودی های جزئی بیشتری تجزیه شود، خروجی سیستم از طریق برهم زدن خروجی های جزئی تولید شده توسط این ورودی های جزئی (خاصیت افزودنی) بدست می آید.

پ) با توجه به نحوه در نظر گرفتن زمان، مدل های زیر برجسته می شوند:

• مدل های گسسته
• مدل های مداوم.

ثابت شده است که سیستم ها دارای یک شخصیت پویا هستند، ورودی، خروجی و حالت های سیستم توابع زمان t هستند. بدیهی است که متغیر t پیوسته متعلق به اعداد واقعی است و بنابراین سیستمهای واقعی در برابر زمان پیوسته هستند. استفاده از مدلهای پیوسته مشکلات خاصی ایجاد می کند. به همین دلیل است که در عمل، مدل های گسسته به طور مکرر مورد استفاده قرار می گیرند، متغیر t گسسته می شود. این تقریب فرآیندهای مداوم از طریق مدل های گسسته امکان استفاده از روش های حل عددی را فراهم می کند.

در هیدرولوژی و مدیریت آب و همچنین در مورد سایر سیستم های فنی، گسسته شدن محور زمان در فواصل زمانی که مقدار آن به فرآیند تحلیل شده بستگی دارد، مکرر است. به عنوان مثال، در مورد طغیان زیاد، این فاصله در عملکرد حوزه حوضه رودخانه، مقادیر را از یک تا چند ساعت می گیرد. برای تخصیص منابع آب از یک مخزن، مرحله زمانی معمولاً یک ماه است. برای سفره های زیرزمینی منطقه، مرحله گسسته سازی ممکن است حتی به 2-3 ماه برسد.

ت) با توجه به میزان دانش سیستم های تجزیه و تحلیل شده، از مدل های زیر استفاده می شود:

• مدل های مبتنی بر فیزیک (مدل های جعبه سفید)؛
• مدل های مهندسی از انواع مختلف:
• مدل های ورودی-خروجی (جعبه سیاه)؛
• مدلهای ابتدایی ورودی-خروجی؛
• مدل های مفهومی (جعبه خاکستری).

مدل های مبتنی بر فیزیک، یک فرایند یا پدیده را از طریق برخی معادلات دیفرانسیل یا معادلات با مشتقات جزئی، به دقت توصیف می کنند. راه حل ها با یکپارچه سازی تحلیلی یا عددی بدست می آیند. فرآیندهای فیزیکی تشکیل رواناب در دامنه ها یا روند نفوذ آب به خاک را می توان با چنین مدل هایی بررسی کرد. در حقیقت، این مدل ها مدل های مبتنی بر فیزیک ورودی-خروجی هستند. آنها کاملاً پدیده یا روند تحلیل شده را منعکس می کنند، با پیچیدگی و ضمنی با حل دشوار مشخص می شوند. برای کالیبراسیون پارامترهای این مدل ها، اندازه گیری های آزمایشی لازم است.

هدف از مدلهای مهندسی، بدست آوردن خروجی O(t) در تابع ورودی I(t)، بدون مطالعه دقیق فرایندهای داخلی سیستم است.

تابعی را که در چارچوب نوع مدلهای جعبه سیاه، ورودی را به خروجی تبدیل می کند، عملکرد هسته یا عملکرد توزین می نامند. روابط در حال استفاده، عبارات ریاضی مختلفی دارند، زیرا متغیرها ممکن است گسسته یا پیوسته باشند.

برای متغیرهای پیوسته، خروجی O(t) با استفاده از انتگرال کانولوشن محاسبه می شود، همچنین یکپارچه Duhamel نامیده می شود:

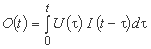
جایی که U(t) نشان دهنده عملکرد وزن است.

این انتگرال دارای ویژگی تقارن زیر است:

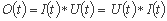
به این معنی که:

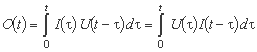
در مورد متغیرهای گسسته، انتگرال کانولوشن به شرح زیر است:

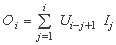
که در آن Ui مقادیر مجزا از تابع وزن است.

گسترده ترین عملکرد وزنی در هیدرولوژی هیدروگراف واحد است که در مدل سازی فرآیندهای هیدرولوژیکی استفاده می شود.

اگر درون ورودی و توابع خروجی با تبدیلات لاپلاس خود جایگزین شوند، مفهوم تابع انتقال استفاده می شود. در این حالت، رابطه بین ورودی و خروجی به شرح زیر نوشته می شود:

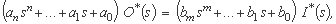
جایی که:

 a_i پارامترهای متصل به مقادیر خروجی؛

 s یک متغیر پیچیده است.

 O*(s) مقدار خروجی؛

 b_i پارامترهای مشخص کننده ورودی مدل؛

I*(s) مقدار ورودی می باشد.

نسبت بین تبدیلات لاپلاس در خروجی و ورودی سیستم:

=

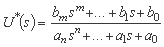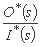
با تعریف، عملکرد انتقال سیستم را نشان می دهد و اجازه می دهد تا ورودی I * (s) را به خروجی O * (s) تبدیل کنیم:

 = 

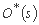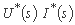
ما در اینجا یادآوری می کنیم که تبدیل Laplace یک تابع f (t) تابع Φ (s) است که توسط انتگرال تعریف شده است:

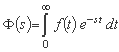
نام تابع انتقال حتی در مواردی که متغیرهای ورودی و خروجی به صورت اعداد واقعی بیان می شوند، قابل استفاده است. حتی ضریب رواناب که نسبت بین بارش موثر و بارش کل است، یک عملکرد انتقال را نشان می دهد. هر عملگر، اگر در ورودی اعمال شود، آن را به خروجی تبدیل می کند، ممکن است به عنوان یک تابع انتقال در نظر گرفته شود.

به عنوان مدل های ابتدایی حالت های ورودی - خروجی در هیدرولوژی متداول ترین مدل هایی هستند که ضریب رواناب برای آنها به تکامل رطوبت خاک بستگی دارد، که وضعیت سیستم را مشخص می کند.

مدلهای مفهومی شامل جزئیات فرایندهایی است که در سیستم اتفاق می افتد، پس از تجزیه آن به عناصر. تکامل از مدلهای ابتدایی ورودی-خروجی یا حالتهای ورودی-خروجی به مدلهای مفهومی در واقع معادل دهانه (یا روشنایی) جعبه سیاه است. اجزای سیستم به صورت سری یا موازی به یکدیگر متصل می شوند. هر م componentلفه ورودی خود را در خروجی خاص تغییر می دهد. مدلهای مفهومی استفاده از توابع هسته را انتقال می دهند یا عملکردها را از سطح سیستم به سطح زیر سیستم منتقل می کنند، که به آنها امکان می دهد تعمیم مدلهای قبلی در نظر گرفته شوند.

نام مدلهای مفهومی به روشی است که در آن مکانیسمهای تغییر شکل خاص هر مولفه و همچنین پیوندهای بین مولفه ها تصور یا تصور می شود.

نمونه های معمولی مدل های مفهومی در هیدرولوژی مدل های مخزنی هستند. آب حاصل از رسوبات به طور پی در پی از طریق یک سری مخازن به هم پیوسته (لایه گیاهی، مخزن برف، لایه خاک، سفره آب، شبکه هیدروگرافی) انجام می شود که هر مخزن طبق قوانین خاص خود تخلیه می شود.

ث) در مورد روش بررسی تنوع پارامترها، موارد زیر برجسته می شوند:

• مدل هایی با پارامترهای جهانی (یا توده ای).
• مدل هایی با پارامترهای توزیع شده.

در مورد مدلهای دارای پارامترهای برآمدگی، مقادیری که ساختار سیستم را مشخص می کنند، مقدار شارهای ورودی و خروجی و همچنین مقادیر حالت برای کل سیستم ثابت است، در حالی که برای مدلهای دارای پارامترهای توزیع شده، همان مقادیر در فضا متغیر هستند.

مدل های دارای پارامترهای جهانی در موارد زیر استفاده می شوند:

• درجه همگن بودن سیستم بالا است.
• ساختار سیستم نسبتاً ناشناخته است و حالتهای داخلی سیستم یا برای اندازه گیری قابل دسترسی نیستند، یا علاقه عملی ندارند.

چنین مدلهایی ممکن است به عنوان مثال برای ارزیابی تخلیه در یک قسمت خاص در رودخانه استفاده شود. عناصر ورودی (رسوبات، دما) یا حالت سیستم (رطوبت خاک) بر روی سطح حوضه رودخانه به طور متوسط ​​ساخته می شوند، ساختار ناهمگن آن نادیده گرفته می شود.

فرضیه های ساده سازی، که در اساس مدل هایی با پارامترهای جهانی قرار دارند، منجر به کاهش درجه دقت بیشتری می شوند، اما نتایج به دست آمده در بسیاری از شرایط رضایت بخش است.

در صورت ناهمگنی زیاد سیستم، ممکن است پارامترهای مدلهای متناظر ثابت نباشند، اما در فضا متغیر باشند، مدلهای حاصل با پارامترهای توزیع شده. سیستم از نظر فضایی (و نه عملکردی) در مناطق شبه همگن گسسته می شود و هر منطقه با مقادیر خاص پارامترهای آن مشخص می شود. با این حال باید ذکر شود که در یک منطقه پارامترها یک شخصیت جهانی دارند، دقیقاً مانند داده های ورودی یا متغیرهای حالت که مقادیر میانگین هر یک از این مناطق را دارند.

اولین مدل های دارای پارامترهای توزیع شده در علوم هیدرولوژیکی برای مدل سازی منابع آب زیرزمینی استفاده شده است، سفره های زیرزمینی با یک متغیر هدایت هیدرولیکی در فضا مشخص می شوند. برای مدل سازی ریاضی، دامنه مطالعه گسسته می شود. هر عنصر از مش می تواند در یک حد خاص خاصیت هدایت هیدرولیکی داشته باشد، شارژ مجدد بارش متر یا ضریب ذخیره

پس از آن، مدل های با پارامترهای توزیع شده شروع به استفاده برای مدل سازی رواناب سطحی نیز می کنند. حوضه های رودخانه در مناطق شبه همگن (مناطق زیر کشت، سطوح پوشیده از جنگل، مناطق غیر قابل نفوذ و غیره) تقسیم می شوند، هر منطقه دارای ساختار تحول خاص و پارامترهای خاص خود است.

با توجه به تعداد زیاد پارامترهای مدل های توزیع شده، پارامترها به طور کلی معنای فیزیکی دارند و ممکن است در داخل بدست آیند. مدل های دارای پارامترهای توزیع شده به دقت بیشتری در مدل سازی منجر می شوند، اما از نظر ارزیابی پارامترها مشکلاتی را به وجود می آورند.

ج) با توجه به درجه دانش سیستم، مدل های ریاضی در این دسته بندی می شوند:

• مدلهای قطعی؛
• مدلهای تصادفی (یا احتمالی).

این مدل زمانی قطعی است که یک ورودی معین همیشه یک خروجی یکسان تولید کند. روابط بین ورودی و خروجی را می توان با استفاده از قوانین فیزیکی، حداقل در یک سطح مربوط به هدف مدل سازی، توصیف کرد. متغیرهای این مدل ها مقادیر قطعی دارند.

برخی از عناصر ورودی تأثیر کم یا ناچیزی بر خروجی دارند. فقط روابط حساس بین ورودی و خروجی باید ارزیابی شود. از دیدگاه عملی، این بدان معنی است که فقط تعداد نسبتاً کمتری از عناصر ورودی به عنوان ورودی مناسب در نظر گرفته می شوند که از طریق وابستگی های علی قوی به خروجی مرتبط می شوند. عناصر ورودی باقی مانده نادیده گرفته می شوند و یا اغتشاشات (سر و صدا) در نظر گرفته می شوند، که باعث ایجاد انحراف از رفتار دقیق سیستم تعیین کننده می شود.

اگر صداها مهم هستند، باید تحقیق را بزرگتر کرد (یک یا چند ورودی قابل توجه نادیده گرفته شده اند)، یا یک جز random تصادفی (یا تصادفی) را معرفی می کند.

این مدل زمانی تصادفی می شود که از قوانین احتمالی استفاده شده و عناصر تصادفی با توزیع مشخص یا قابل تعیین در مدل رخ دهند.

مدل های تصادفی را می توان به موارد زیر تقسیم کرد:

• مدل هایی برای تجزیه و تحلیل فرکانس (تجزیه مجدد آماری).
• مدل های رگرسیون.
• مدل های تصادفی.
• مدل هایی با ضرایب تصادفی.
• مدلهایی با محدودیتهایی که در احتمال بیان می شوند (مدلهای محدود شانس).

مدل های تجزیه و تحلیل فرکانس به طور کلی در هیدرولوژی برای ارزیابی مقادیر مشخص شده با احتمال بیش از حد معین (یا با دوره بازگشت مربوطه) استفاده می شود. برای اندازه گیری سرریز سد، از سیلابهای استثنایی با فرکانس نادر استفاده می شود. برای بدست آوردن حداکثر تخلیه با احتمال بیش از حد مشخص، پردازش آماری حداکثر تخلیه های سالانه ضروری است، و از طریق تجزیه مجدد نظری، تقسیم تجربی را برون یابی می کنیم.

از مدل های رگرسیون برای بررسی وابستگی یا استقلال دو یا چند متغیر آماری استفاده می شود. اگر متغیرها مستقل باشند، ممکن است بصورت جداگانه یک بعدی تجزیه و تحلیل شوند. اگر متغیرها وابسته باشند، ارزیابی تأثیر یک متغیر (یا گروهی از متغیرها) بر متغیر توضیح داده شده مهم است. این پردازش آماری از اهمیت عملی ویژه به عنوان تجزیه و تحلیل همبستگی یا رگرسیون شناخته می شود.

منحنی های رگرسیون بین دو متغیر دارای اهمیت برخی از مقادیر متوسط ​​شرطی هستند. شدت وابستگی آماری بین متغیرها با ضریب همبستگی در مورد همبستگی خطی و با نسبت همبستگی برای یک همبستگی غیر خطی بیان می شود.

همبستگی ها از اهمیت ویژه ای در هیدرولوژی برخوردارند. یکی ممکن است به عنوان مثال:

• منحنی رتبه بندی (همبستگی H-Q) ؛
• ارتباط بین ضریب تبخیر و ارتفاع ؛
• ارتباط بین زمان افزایش سیل زیاد و متغیر 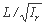 جمع شده، و  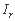شیب رودخانه است.
• همبستگی بین کل مدت زمان طغیان زیاد و یکی از متغیرهای زیر (ساده یا جمع شده): L، 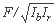 یا 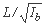 (جایی که L طول رودخانه است، I_b شیب حوضه رودخانه است، F سطح حوضه و غیره است).

مقادیر متغیر توضیح داده شده انحرافات موجود در مقایسه با مقادیر متوسط ​​نشان داده شده توسط منحنی همبستگی است. هرچه مقادیر مربوطه به منحنی نزدیکتر باشند، وابستگی بین متغیرها بیشتر خواهد بود. در این حد، اگر تمام مقادیر روی منحنی قرار بگیرند، پیوند بین متغیرها تعیین کننده است.

یک فرآیند تصادفی نشان دهنده یک ردیف بی نهایت از متغیرهای آماری است. یک نمونه محدود از این سطر یک سری زمانی نامیده می شود و در واقع یک متغیر آماری چند بعدی است.

اگر همه متغیرهای آماری که این مجموعه را تشکیل می دهند توزیع یکسانی داشته باشند، سری زمانی مربوطه نمونه ای از یک فرآیند تصادفی ثابت را تشکیل می دهد. اگر اجزای سری زمانی قانون توزیع یکسانی داشته باشند، اما با پارامترهای مختلف (مقدار متوسط ​​، پراکندگی)، فرآیند تصادفی مربوطه غیر ثابت است.

مشاهدات مربوط به یک فرآیند تصادفی ممکن است یک روند تکامل کلی را نشان دهد، نمایانگر مولفه قطعی مجموعه (که به آن مولفه  یا گرایش سیستماتیک نیز گفته می شود) که به دلیل برخی عوامل با تأثیر تصادفی، یک مولفه  آماری به آن اضافه می شود.

مولفه  قطعی به طور کلی توسط یک گرایش چند جمله ای شکل می گیرد، که به تدریج از نظر زمان متغیر است و از آن اجزای فصلی می آیند که به صورت دوره ای خود را نشان می دهند. این دوره معمولاً روز، ماه، فصل، سال است، اما همچنین می تواند گروه هایی از سالها یا قرن ها باشد.

مولفه  آماری این فرآیند پس از کسر مولفه  قطعی از سری اولیه، تجزیه و تحلیل می شود. باقیمانده ها (تفاوت بین سری اولیه و مولفه  قطعی) مانند یک سری زمانی تفسیر می شوند، که از یک فرآیند تصادفی ثابت استخراج شده اند.

فرآیندهای تصادفی به طور کلی و سری زمانی بخصوص در هیدرولوژی استفاده می شود. بنابراین، تخلیه ها ممکن است به عنوان یک فرآیند مارکوف تفسیر شوند. نسل مصنوعی مقادیر هیدرولوژیکی در واقع برای مدتی طولانی در عمل مورد استفاده قرار گرفته است (M. Fiering, 1967) بر اساس مدل مارکوف.

توالی داده های هیدرولوژیکی ثبت شده در گذشته همه موارد ممکن را برای اندازه گیری یا ایجاد قوانین بهره برداری برای کارهای مدیریت آب ارائه نمی دهد. گسترش داده های موجود توسط تولید مصنوعی با استفاده از مدل های مارکوف یا سری های زمانی (با رعایت ویژگی های اساسی داده های اولیه: مقدار متوسط ​​، ضریب تغییر و عدم تقارن) تا حد زیادی انجام می شود. این تکنیک ها منجر به اطلاعات جدیدی در مورد هیدرولوژی رودخانه نمی شوند. آنها فقط اجازه می دهند سناریوهای مختلف تخلیه، اطلاعات اولیه یا بیشترین قسمت آن را بدست آورند.

مدلهایی با ضرایب تصادفی زمانی استفاده می شوند که ضرایب خاصی از مدلهای ریاضی دارای مقدار منحصر به فردی نباشند، اما طیف وسیعی از مقادیر را با احتمالات مختلف می گیرند. بنابراین، مقادیر بدست آمده از اندازه گیری ها در معرض خطا هستند. از طرف دیگر، برخی از متغیرها به دلیل ماهیت خاص خود (تخلیه، هزینه و غیره) دارای ویژگی تصادفی هستند. با در نظر گرفتن آن، مدل واقع گرایانه تر می شود، اما حل آن نیز دشوارتر می شود.

مدلهای دارای محدودیتهایی که به احتمال زیاد بیان می شوند، خود را هنگامی تحمیل می کنند که محدودیتهای خاصی همیشه برآورده نشوند. چنین شرایطی اغلب در زمینه مدیریت آب وجود دارد. برخی از اهداف (تأمین آب برای کاربران، کنترل سیل، محافظت از کیفیت آب) ممکن است همیشه با اطمینان محقق نشود، اما با یک احتمال خاص. از این دیدگاه، یک مدل قطعی را می توان یک مدل احتمالی دانست، که روابط آن با احتمال 100٪ راضی است.

چ) با توجه به تعداد اجزای ورودی و خروجی، مدلها را می توان در:

• تک متغیر
• چند متغیره

یک ورودی و یک خروجی مدل های تک متغیری را مشخص می کند، در حالی که مدل های چند متغیره ورودی و یک یا چند خروجی بیشتر دارند.

یک نمونه از مدل های تک متغیر در هیدرولوژی استفاده از میانگین بارش جهانی در مقیاس یک حوزه آبخیز است که نشان دهنده یک مقدار ورودی منحصر به فرد در مدل های هیدرولوژیکی است. اگر یکی به هر ایستگاه یک چند ضلعی Thiessen مرتبط کند، یک مدل چند متغیره با مقادیر ورودی بیشتر بدست می آورد. ملاحظات مشابهی ممکن است در مورد منطقه بندی مجدد شارژ آبخوان نیز داده شود.

ح) از نظر تعداد پارامترها، مدل های زیر برجسته می شوند:

• مدل های غیر پارامتری.
• مدلهای پارامتری.

جداول و همچنین منحنی ها یا مجموعه ای از منحنی ها، که به صورت گرافیکی نشان داده شده اند یا مختصات آنها به صورت عددی تعریف شده است، در دسته مدل های غیر پارامتری قرار دارند. می توان نمونه هایی از مدل های غیر پارامتری را ذکر کرد: قوانین بهره برداری از یک مخزن، منحنی های SSARR، قوانینی برای تخصیص آب و غیره .

مدلهای ورودی-خروجی که تغییر شکل ورودی در مقادیر خروجی تحت فرم تحلیلی بیان می شود و همچنین مدلهای ورودی-خروجی که به صورت معادلات حالت نوشته می شوند، نمونه هایی از مدلهای پارامتری هستند. اتاق مطالعه فرایندهای d با معادلات دیفرانسیل، در مورد مدلهای دارای پارامترهای جهانی، یا با معادلات با مشتقات جزئی، در مورد مدلهای با پارامترهای توزیع شده، توصیف می شوند. ضرایب معادلات پارامترهایی را نشان می دهند که باید تخمین زده شوند. هرچه مدل مقاوم تر باشد، تعداد کمتری از پارامترها باید کالیبره شوند (اصل تجزیه پارامترها). تابع انتقال، به صورت تحلیلی تعریف شده، نمونه دیگری از مدل پارامتری است.

تابع توزین تعریف شده با مقادیر گسسته یک مدل غیر پارامتری است. ممکن است در یک مدل پارامتری، به دنبال انحناهای تحلیلی تعریف شده، که به خوبی با مختصات تابع وزنی متناسب هستند، به روشی نسبتاً ساده تبدیل شود.

اگر بیان تحلیلی تابع وزنی مشخص باشد، پارامترهای آن می توانند مستقیماً از طریق بهینه سازی تعیین شوند.

خ) با توجه به هدف مدل سازی، مدل ها را برای موارد زیر متمایز می کند:

• شبیه سازی سیستم
• بهینه سازی سیستم

مدل های شبیه سازی به عنوان آخرین هدف برای پیش بینی تکامل یک سیستم تحت عمل برخی از عوامل مزاحم یا پیش بینی نتایج برخی تصمیمات است. در حال حاضر در مطالعه پویایی سیستم های پیچیده از مفهوم شبیه سازی استفاده می شود. شبیه سازی ممکن است تقلیدی، قیاسی یا ریاضی (عددی) باشد.

شبیه سازی عددی بیانگر یک تکنیک برای تحقق آزمایشات با استفاده از مدل های ریاضی و کدهای رایانه ای مربوطه برای توصیف رفتار یک سیستم واقعی (یا برخی از اجزای آن) در طی یک دوره زمانی خاص است. مدل های شبیه سازی به ویژه انعطاف پذیر هستند، به شما اجازه می دهند تعداد زیادی از متغیرها و برخی پیوندهای بسیار پیچیده بین اجزای سیستم را در نظر بگیرید. بدیهی است، این جزئیات سیستم مورد بررسی منجر به مقدار قابل توجهی از محاسبات می شود. مدلهای ریاضی در حالت غیر ثابت برای مسیریابی سیلاب یا مدلهای شبیه سازی حرکت آب زیرزمینی ممکن است در اینجا ذکر شود.

اهداف اصلی شبیه سازی عبارتند از: (Shanon, 1975):

• برای توصیف رفتار سیستم ها
• پیشنهاد فرضیه ها و نظریه ها برای توضیح تکامل مشاهده شده.
• استفاده از این فرضیه ها و نظریه ها برای پیش بینی های مربوط به تکامل آینده سیستم.

مدل های بهینه سازی برای بهبود رفتار سیستم در یافتن قوانین عملکرد بهتر و همچنین برای ارزیابی بهتر پارامترهای موجود در ساختار مدل های ریاضی استفاده می شوند.

از نظر ریاضی، فرایند بهینه سازی شامل تعیین برخی از افراط است، متغیرهای سیستم و حالاتی که برخی از محدودیت های نظم فیزیکی یا عملکردی را برآورده می کنند. در نتیجه، تجزیه و تحلیل ریاضی کلاسیک با تکنیک های برنامه نویسی ریاضی (برنامه ریزی خطی، غیر خطی، پویا، برنامه نویسی به تعداد عدد صحیح، حداکثر اصل پونتریاگین و غیره) جایگزین می شود.

یک مدل بهینه سازی، جدا از معادلات جبری یا دیفرانسیل منعکس کننده پویایی سیستم یا پیوندهای بین متغیرها، محدودیت هایی در مورد دامنه تغییر آنها و همچنین یک تابع هدف (عملکرد معیارها، تابع هدف، تابع بهینه سازی، عملکرد، شاخص عملکرد و غیره.).

مدیر سایت: بهزاد سرهادی

شماره تلفن: 09190622992

شناسه تلگرام مدیر سایت: SubBasin@

نشانی ایمیل: behzadsarhadi@gmail.com

(سوالات تخصصی را در گروه تلگرام ارسال کنید)

_______________________________________________________

پروژه تخصصی در لینکدین

×

 براي پيوستن به بزرگترين گروه تلگرام علوم و مهندسي آب با امکان تبادل نظر بين اعضاء کليک کنيد

کتاب کاربرد مدل QUAL2KW

کتاب کاربرد GIS در منابع آب

کتاب محاسبه سيل طرح