1.6 معادلات سنت ونانت

برای بسیاری از کاربردهای عملی، تغییر فضایی سرعت در سطح مقطع جریان را نمی توان نادیده گرفت، بنابراین می توان روند جریان را تغییر داد که فقط در جهت طولی جریان متغیر است. این فرض اصلی است که برای استخراج معادلات Saint-Vénant استفاده شده است، که جریان ناپایدار کانال باز یک بعدی را توصیف می کند.

فرضیه های برخی دیگر نیز لازم است. در شکل اصلی خود (B. de Saint-Vénant, 1871)، اینها به شرح زیر است:

• سرعت در هر بخش عمود بر محور طولی ثابت است،
• انحنای ساده کوچک و شتاب های عمودی ناچیز است، به طوری که فشار هیدرواستاتیک غالب است،
• اثرات اصطکاک مرزی و تلاطم را می توان از طریق روابط مقاومتی مشابه آنچه برای جریان حالت پایدار استفاده می شود، حساب کرد.
• شیب پایین کانال متوسط ​​کم است به طوری که کسینوس زاویه ایجاد شده با افقی را می توان با واحد تغییر داد.

به منظور شفافیت، کتابهای درسی مختلف (Cunge، Holly and Verwey، 1980؛ Chow، Maidment and Mays، 1988؛ Popa، 1997 و غیره) برخی از فرضیات واضح را برجسته می کنند به عنوان مثال: بستر کانال ثابت است (بدون اثرات رسوب). مقاطع عرضی شکل دلخواهی دارند و ممکن است در امتداد محور کانال تغییر کنند (اما در محدوده محدود). و غیره.

تحت این مفروضات، معادلات اساسی سن ونت را می توان با چندین روش بدست آورد (نگاه کنید به Strelkoff, 1969؛ Cunge a.o., 1980؛ Graf and Altinakar, 1996؛ و غیره). این ماده از مطالعات Chow a.o پیروی می کند که در سال (1988) مطرح شد، و به دلیل کلی بودن و سادگی آن، ارائه شده است.

معادله تداوم

یک حجم کنترل اساسی (c.v) طول dx را در یک رودخانه در نظر بگیرید. اگرچه اندازه فضایی آن ثابت است، اما سطح آب ممکن است به مرور زمان تغییر کند.

معادله تداوم برای جریان ناپایدار چگالی متغیر از طریق این c.v را می توان اینگونه نوشت (برای نمایش قضیه انتقال رینولدز در توده خاصیت مایع اعمال شده به مطالعات Chow و همکاران, 1988، یا Popa, 1998 مراجعه کنید):

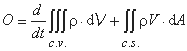
جایی که:

•  c.s. سطح c.v ابتدایی را مشخص می کند.
•  dA مساحت اولیه c.s.
•  V سرعت محلی جریان است.

شکل 1.6 سه نمای از این دسترسی اولیه کانال را نشان می دهد.

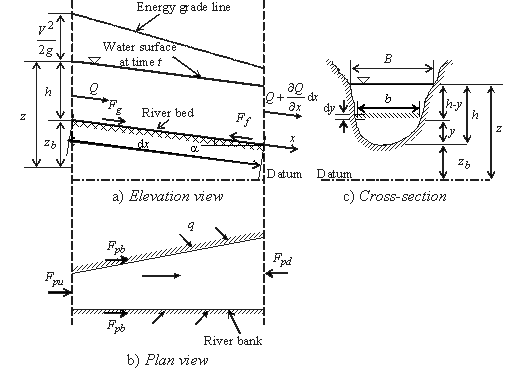
شکل 1.6 طرح تعریف برای استخراج معادلات جریان ناپایدار.

با استفاده از قرارداد علامت مانند قضیه انتقال رینولدز (به عنوان مثال "-" برای ورودی ها و "+" برای خروجی ها در یا از c.v.)، آخرین اصطلاح برای تعادل جرم در معادله بالا این است:

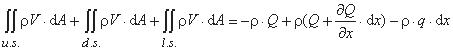
جایی که:

•  Q دبی جریان که وارد c.v می شود. توسط سطح بخش بالادست (u.s.)
•  ∂Q/∂x سرعت جریان در امتداد محور جریان تغییر می کند، به طوری که جریان خروجی توسط سطح مقطع پایین دست (d.s.) می شود (Q + (∂Q/∂x)dx)
•  q با ورود به c.v به عنوان ورودی جانبی در واحد طول کانال پذیرفته می شود. سطح جانبی (l.s.) توسط رواناب در حاشیه، نفوذ از آبهای زیرزمینی و غیره

با فرض یک سطح مقطع متوسط ​​A، حجم c.v. برابر dV=Adx است، به طوری که میزان تغییر جرم ذخیره شده در c.v. (اولین شرط در معادله اول) را می توان به صورت زیر نوشت:

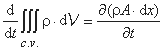
جایی که مشتق جزئی وابستگی به زمان سطح آب را در نظر می گیرد.

با جایگزینی معادلات، پذیرفتن تراکم آب به صورت ثابت و تقسیم بر اساس، فرم حفاظت از معادله پیوستگی به شرح زیر است:

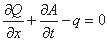
که برای شکل منشوری (با شکل مقطع ثابت و شیب بستر در امتداد کانال) یا یک آبراه غیر منشوری ارزش دارد.

معادله حرکت

حرکت لحظه ای حاصل جرم و سرعت است و شار حرکت در قسمت جریان حاصل سرعت جریان جرم و سرعت است. با نوشتن قانون دوم نیوتن به شرح زیر:

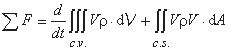
می توان بیان کرد که مجموع نیروهایی که به c.v اعمال می شود باید برابر با سرعت تغییر حرکت ذخیره شده در c.v باشد. به علاوه خروج خالص حرکت در سراسر c.s.

در مورد آخرین عبارت در معادله بالا و با شبیه سازی با معادله اولیه یکی بدست می آید:

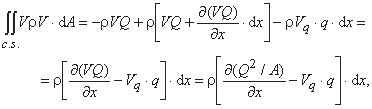
که در آن Vq جز سرعت q در جهت جریان است (0 - برای ورودی جانبی عمود).

سرعت تغییر زمان حرکت ذخیره شده در c.v. با استفاده از آن dV = A.dx و به عنوان مثال یافت می شود:

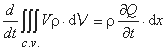
به منظور سادگی، فقط نیروهای زیر اعمال شده به c.v. در نظر گرفته می شوند:

F_g - جز وزن آب در امتداد بستر رودخانه (نیروی جاذبه)، داده شده توسط:

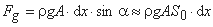
به دلیل فرض کوچک بودن α (به عنوان مثال شیب پایین کانال).

F_f - نیروهای اصطکاک، از جمله اثرات اصطکاک مرزی و تلاطم. به دنبال مطالعات Chow (1959) در کاری تکمیلی Chow a.o در سال (1988) و غیره، F_f به صورت زیر بیان می شود:

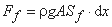
که در آن شیب اصطکاک S_f توسط برخی معادلات مقاومت مورد استفاده برای شرایط جریان ثابت محاسبه می شود.

F_Pu , F_Pd - نیروهای فشار، به ترتیب به عنوان نیروهای هیدرواستاتیک در سطح مقطع بالادست و پایین دست اعمال می شوند.

با استفاده از نمادهای شکل 1.6 جایی که سطح جریان مقطع اولیه b.dy در ارتفاع y از بستر کانال قرار گرفته و دارای عمق غوطه ور (h-y) است، کل فشار هیدرواستاتیک فشار بر سطح مقطع بالادست:

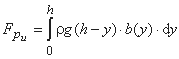
جایی که:

•  b(y) عرض محلی در ارتفاع y
•  h عمق آب

نیروی هیدرواستاتیک در سطح مقطع پایین دست بدست می آید (Chow و همکاران، 1988) به این صورت که:

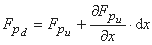
که 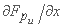 را می توان با استفاده از قانون لایبنیتس برای تمایز یک انتگرال محاسبه کرد، به عنوان مثال:

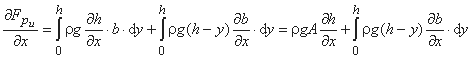
F_Pb - نیروی فشار ناشی از شکل غیر منشوری کانال، یعنی نیرویی که توسط کناره ها اعمال می شود، در رابطه با میزان تغییر عرض کانال، ∂b/∂x در c.v.

بنابراین، این سهم ممکن است به صورت زیر بیان شود:

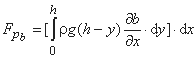
برخی دیگر از تأثیرات احتمالی (به عنوان مثال نیروی برشی باد در برابر سطح عاری از آب، مقاومت موضعی ناشی از تغییر ناگهانی سطح مقطع کانال و غیره) نیز می توانند مدل شوند، اما در این ارائه نادیده گرفته می شوند.

مجموع این نیروها در امتداد x با معادلات حاضر به دست می آید:

 

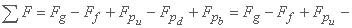
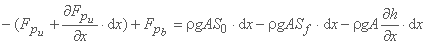
پس از جایگزینی اصطلاحات، فرم حفاظت از معادله حرکت بدست می آید:

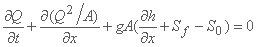
اگر ورودی جانبی به صورت عمود بر جهت جریان اصلی پذیرفته شود.

از آنجا که A = A(h) و dA = B.dh، مشتق زمان ∂A/∂t از معادله بالا را می توان با B.∂h/∂t جایگزین کرد، بنابراین معادله تداوم:

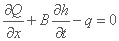
دو متغیر وابسته به معادلات Saint-Vénant فوق عمق آب و دبی جریان Q. برای بسیاری از برنامه ها استفاده از یک جفت متغیر جریان به عنوان متغیرهای اصلی ترجیح داده می شود (Q و z - ارتفاع سطح آب بالاتر از یک داده، برای رودخانه های بزرگ ؛ h و V - سرعت جریان، برای جریان کانال، و غیره). اشکال مربوط به معادلات سنت ونت توسط برخی دستکاری های ساده ریاضی بدست آمده است.

همانطور که h = (z - z_b)) و ∂z_b/∂x = -S₀، مشتق فضا ∂h/∂x از معادله بالا را می توان نوشت: ∂h/∂x = ∂z/∂x + S₀. با توجه به فرض بستر ثابت (z_b- ثابت در زمان)، مشتق زمان ∂h/∂t = ∂z/∂t و جفت Q-z معادلات Saint-Vénant است:

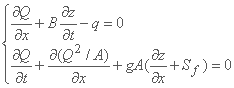
جایگزینی Q = VA در مشتق زمانی به طور متوالی بدست می آید:

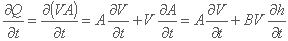
در مورد مشتق فضا ∂Q/∂x، این امر به شرح زیر است:

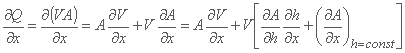
جایی که آخرین اصطلاح در معادله به دلیل شکل مقطع دلخواه است و برای یک کانال منشوری از بین می رود. معادله پیوستگی V-h به این ترتیب است:

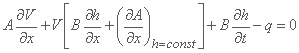
از آنجا که Q²/A = V²A، مشتق ∂(Q²/A)/∂x را می توان به صورت زیر نوشت:

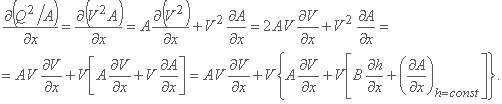
با استفاده از معادلات بالا در معادله لحظه، مرتب سازی مجدد اصطلاحات و پذیرش q = 0، معادله حرکت V-h به دست می آید:

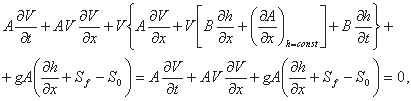
که در آن معادله پیوستگی بین براکت ها اعمال شد {}.

بدون ورودی جانبی و برای مقطع مستطیل (وقتی A = Bh) دو معادله V-h Saint-Vénant به شرح زیر است:

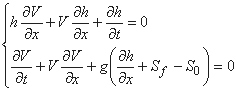
و فرم عدم حفاظت را نام برد.

شیب اصطکاک S_f به صورت حالت پایدار بیان می شود، معمولاً توسط یک رابطه نوع Manning یا Chezy، یعنی:

منینگ:

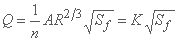
Chezy:

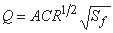
جایی که:

•  n ضریب زبری مانینگ
•  R شعاع هیدرولیکی (= A/P با P: محیط مرطوب)
•  K ضریب انتقال
•  C ضریب مقاومت برقی

مقادیر مناسب Manning's n و Chezy's C پارامترهای تجربی مرتبط با ترکیب بستر رودخانه و رژیم جریان هستند. این مقادیر اغلب به عنوان پارامترهای کالیبراسیون برای یک مدل مسیریابی مشخص پذیرفته می شوند.

مدیر سایت: بهزاد سرهادی

شماره تلفن: 09190622992

شناسه تلگرام مدیر سایت: SubBasin@

نشانی ایمیل: behzadsarhadi@gmail.com

(سوالات تخصصی را در گروه تلگرام ارسال کنید)

_______________________________________________________

پروژه تخصصی در لینکدین

×

 براي پيوستن به بزرگترين گروه تلگرام علوم و مهندسي آب با امکان تبادل نظر بين اعضاء کليک کنيد

کتاب کاربرد مدل QUAL2KW

کتاب کاربرد GIS در منابع آب

کتاب محاسبه سيل طرح