7.6 طرح تفاضل محدود ضمنی برای مدل موج پویا

به دلیل خواص محاسباتی مطلوب، از طرح های ضمنی به طور گسترده در انتشار سیل در امتداد کانال استفاده می شود.

در مرحله اول، یک طرح ضمنی خطی شش نقطه ای در ارتباط با جفت Q-h از معادلات Saint-Vénant ارائه شده است، و در نهایت یک طرح ضمنی غیرخطی چهار نقطه ای برای شرایط طبیعی رودخانه (جفت Q-z) شرح داده شده است.

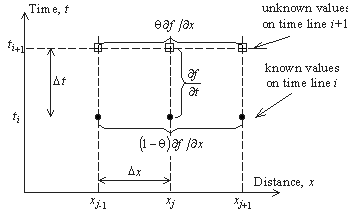
شکل 6.6 سلول اختلاف محدود برای طرح ضمنی شش نقطه.

همانطور که در شکل 6.6 نشان داده شده است، از متغیرهای جریان از شش نقطه شبکه برای تقریب اصطلاحات مشتق شده در معادلات در موقعیت فضای x_j، با عبارات زیر استفاده می شود:

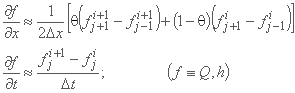
برای اطمینان از ثبات بی قید و شرط طرح، ضریب وزنی θ باید بین 0 و 1 باشد.

به غیر از شیب اصطکاک S_f، اصطلاحات غیرانتقادی با جایگزین می شوند.

برای در نظرگرفتن غیرخطی بودن S_f در رابطه با متغیرهای وابسته Q و h، گسترش سری تیلور این اصطلاح به صورت زیر پذیرفته می شود:

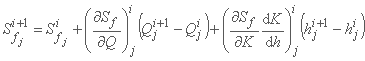
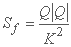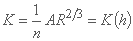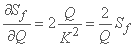 and .

 and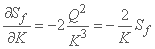 

توجه داشته باشید که (مانند بخش 5.6) از 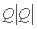اجازه می دهد تا علامت اصطکاک در هر لحظه مطابق جهت جریان محلی باشد.

با استفاده از این تقریب ها در مدل موج دینامیکی دو معادله جبری، خطی و اختلاف محدود زیر در موقعیت مکانی x_j  بدست می آیند:

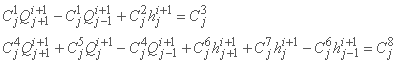
که در آن ضرایب C_j فقط به راه حل شناخته شده در سطح زمانی بستگی دارد. این معادلات شامل شش متغیر وابسته ناشناخته Q و h در x_j و دو نقطه مجاور x_j-1 و x_j+1 می باشد.

برای یک شبکه محاسباتی که دارای موقعیت مکانی N است (بنابراین متغیرهای جریان ناشناخته 2N در هر سطح زمانی)، یک سیستم از 2(N-2) معادلات خطی جبری با نوشتن دو معادله در تمام نقاط شبکه داخلی بدست می آید. چهار معادله لازم باقیمانده با استفاده از فرمهای مشخصه (دو معادله) و شرایط مرزی به ترتیب (همچنین دو معادله) مشتق شده اند. این سیستم معادلات خطی جبری با استفاده از یک روش عددی مناسب حل می شود تا تمام مقادیر ناشناخته Q و h را در سطح زمان فعلی i + 1 بدست آورد.

طرح ضمنی غیرخطی چهار نقطه ای در ارتباط با مدل موج پویای زیر ارائه شده است:

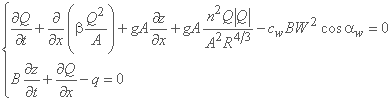
اصطلاح β به عنوان ضریب حرکت (یا بومسینق) شناخته می شود. این توزیع غیر یکنواخت سرعت به سطح مقطع کانال را شامل می شود و مقدار آن از 1.01 (کانال منشوری مستقیم) تا 1.33 (دره رودخانه با دشت های سیلاب) متغیر است. آخرین اصطلاح معادله تکانه مقاومت اصطکاکی باد در برابر سطح آزاد آب را معرفی می کند. سرعت باد W است، در جهت در زاویه α_w نسبت به سرعت آب و c_w یک ضریب اصطکاک است.

این مدل موج پویا همچنین می تواند برای شبیه سازی انتشار سیل در یک سیستم شبکه شاخه از کانال ها استفاده شود و طرح ضمنی چهار نقطه ای چنین کاری را سبک می کند.

یک بخش کانال را در نظر بگیرید که توسط دو مقطع عرضی در موقعیت های x_j و x_j+1 قرار گرفته و دارای طول Δx_j است همانطور که در شکل 7.6 نشان داده شده است. اصطلاحات مختلف معادلات در یک نقطه به عنوان P تقریب می یابند، در فضا متمرکز شده و با توجه به یک عامل وزنی θ در زمان قرار می گیرند.

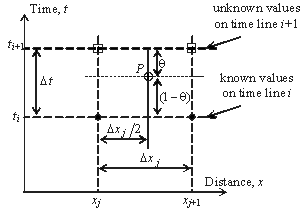
شکل 7.6 سلول اختلاف محدود برای طرح ضمنی چهار نقطه.

مشتقات زمان و مکان به ترتیب به شرح زیر بیان می شوند:

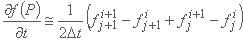
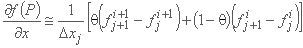
(به استثنای ∂A/∂x، جایی که θ = 1).

اصطلاحات غیر اشتقاقى با تقریب تقریبی:

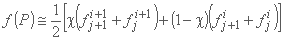
جایی که χ یک عامل وزنی است، شبیه θ.

برای θ > 0، این طرح از نوع ضمنی است و اگر θ > 0.5 باشد، بدون قید و شرط پایدار است. ضریب χ از 0 تا 1 است. اگر χ = 0 باشد، مقدار f منحصراً از مقادیر گام زمان قبلی به دست می آید، در حالی که χ = 1 یک تقریب کاملاً رو به جلو برای f تولید می کند.

اگر χ ≠ 0 باشد، به دلیل وابستگی آن به متغیرهای جریان ناشناخته در خط زمان (i + 1)، یک غیرخطی ظاهر می شود. همراه با اصطلاح غیرخطی از 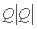 شیب اصطکاک، این جنبه رویه تکراری را در هر مرحله زمان تحمیل می کند. در تکرار اول  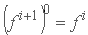پذیرفته می شود، در حالی که برای تکرار بعدی معادله بالا با این جایگزین می شود:

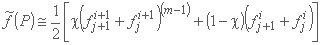
با m یک شاخص تکرار.

این شرط 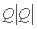 به این صورت  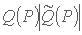بیان می شود که در آن معادله بالا برای Q (P) و به ترتیب معادله آخر برای  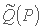استفاده می شود.

سپس دو معادله Saint-Vénant با معادلات اختلاف محدود زیر جایگزین می شوند:

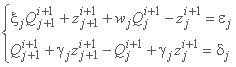
جایی که:

;

;;

;;;

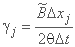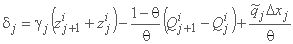
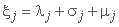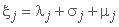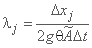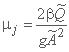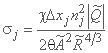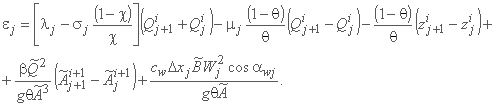
ضرایب فوق همه از مقادیر شناخته شده در مرحله زمان قبلی یا تکرار قبلی در مرحله زمان ارزیابی می شوند.

تعریف بردار حالت دو جزئی در سطح مقطع i به عنوان:

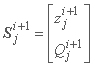
می توان معادلات حاضر را به عنوان معادله تبدیل ماتریس برای بخش j-th نوشت:

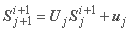
که در آن چهار عنصر ماتریس وجود دارد:

;;

;;

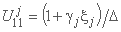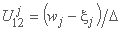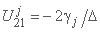
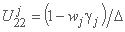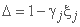و دو عنصر ماتریس u_j عبارتند از:

;

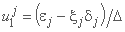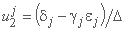
از طریق استفاده متوالی از معادله تبدیل-بخش، اکنون می توان یک معادله تحول شاخه را به صورت زیر بدست آورد:

جایی که ماتریس های تغییر شکل شاخه U_b و u_b است داده شده توسط:

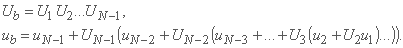
در اینجا یک شاخه یک رودخانه است که به تعدادی از بخشهای محاسباتی Δx_j, j = 1.........., N-1 تقسیم می شود همانطور که در شکل 8.6 آمده است.

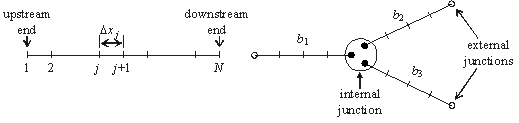
شکل 8.6 یک سیستم واحد شاخه ای (الف) و شبکه ای از شاخه های (ب).

اگر مسئله جریان به یک سیستم شاخه ای واحد اشاره داشته باشد، دو معادله غیرخطی جبری مربوط به معادله ماتریس با دو معادله شرط مرزی تکمیل می شوند. سیستم حاصل از معادلات حل شده است تا چهار مقدار Q و z ناشناخته را در مقطع شدید 1 و N، با تکرار فعلی در خط زمانی i + 1، بدست آورد. تمام مقدار متغیرهای جریان واسطه می توانند با استفاده از معادله تبدیل-تبدیل به طور متوالی حاصل شوند. فرآیند تکراری تا زمان تحقق معیار همگرایی تکرار می شود.

اگر مسئله جریان در شبکه ای از شاخه ها ظاهر شود، همانطور که در شکل بالا نشان داده شده است، معادلات ماتریس تغییر شکل شاخه برای هر شاخه نوشته شده و شش معادله جبری مربوطه باید با شرایط مرزی در سه اتصال خارجی، به علاوه شرایط سازگاری در محل اتصال داخلی (یعنی جریان تعادل تخلیه و برابری سطح سطح آب). با حل سیستم معادلات حاصل، تخلیه ها و مراحل ناشناخته در شش انتهای شاخه ها استخراج شده و محاسبه مجدداً برای یک مورد تک شاخه از سر گرفته می شود.

این طرح ضمنی غیرخطی چهار نقطه ای توصیه می شود (Schaffranek، Baltzer، Goldberg, 1981) به دلیل کارایی محاسباتی ذاتی، پایداری و انعطاف پذیری با توجه به استفاده از شرایط مرزی خارجی و داخلی.