مدل های چند لایه پرسپترون برای پیش بینی سری زمانی داده آب

پرسپترون چند لایه یا به اختصار MLP می توانند برای پیش بینی سری زمانی استفاده شوند. چالشی در استفاده از MLP برای پیش بینی سری زمانی در تهیه داده ها وجود دارد. به طور خاص، مشاهدات تأخیر (لگ) مشاهداتی باید به بردارهای اجزا مسطح شود. در این آموزش، شما می آموزید که چگونه مجموعه ای از مدل های MLP را برای طیف وسیعی از مسائل پیش بینی سری زمانی استاندارد ایجاد کنید. هدف این آموزش ارائه نمونه های مستقل از هر مدل در مورد هر نوع مسئله سری زمانی به عنوان الگویی است که می توانید آن را کپی کرده و برای مشکل پیش بینی سری زمانی خاص خود تطبیق دهید.
پس از اتمام این آموزش، خواهید آموخت که:
- چگونه می توان مدل های MLP را برای پیش بینی سری زمانی تک متغیره توسعه داد.
- چگونه می توان مدل های MLP را برای پیش بینی سری زمانی چند متغیره توسعه داد.
- چگونه می توان مدل های MLP را برای پیش بینی سری های زمانی چند مرحله ای توسعه داد.
بررسی اجمالی آموزش
این آموزش به چهار قسمت تقسیم شده است:
- مدل های MLP تک متغیره
- مدل های MLP چند متغیره
- مدل های MLP چند مرحله ای
- مدل های MLP چند مرحله ای چند متغیره
مدلهای MLP تک متغیره
از پرسپترون چند لایه یا به اختصار MLP می توان برای مدل سازی مسائل پیش بینی سری زمانی تک متغیره استفاده کرد. سری های زمانی تک متغیره یک مجموعه داده متشکل از یک سری مشاهدات با یک ترتیب زمانی است و برای پیش بینی مقدار بعدی در توالی، یک مدل برای یادگیری از مجموعه مشاهدات گذشته مورد نیاز است.
این بخش به دو قسمت تقسیم شده است:
- آماده سازی داده ها
- مدل MLP
آماده سازی داده ها
قبل از مدل سازی یک سری تک متغیره، باید آن را تهیه کنید. مدل MLP تابعی را فرا می گیرد که توالی مشاهدات گذشته را به عنوان ورودی برای مشاهده خروجی ترسیم می کند. به همین ترتیب، توالی مشاهدات باید به چندین نمونه تبدیل شود که مدل می تواند از آنها یاد بگیرد.
یک توالی تک متغیر را در نظر بگیرید:

ما می توانیم توالی را به چندین الگو ورودی / خروجی به نام نمونه تقسیم کنیم، جایی که سه مرحله زمان به عنوان ورودی و یک مرحله زمان به عنوان خروجی برای پیش بینی یک مرحله ای که آموخته می شود، استفاده می گردد.

تابع split_sequence در زیر این رفتار را پیاده سازی می کند و یک توالی تک متغیر داده شده را به چندین نمونه تقسیم می کند که در آن هر نمونه تعداد مشخصی از مراحل زمانی را دارد و خروجی یک مرحله واحد است.

ما می توانیم این عملکرد را در مجموعه داده کوچک ساختگی خود در بالا نشان دهیم.
مثال کامل در زیر ذکر شده است:
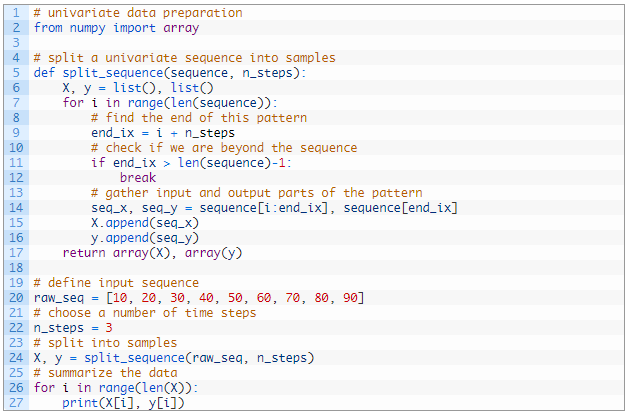
با اجرای مثال ، سری تک متغیره به شش نمونه تقسیم می شود که هر نمونه دارای سه مرحله زمان ورودی و یک مرحله زمان خروجی است.

اکنون که ما می دانیم چگونه یک سری تک متغیره را برای مدل سازی آماده کنیم، بیایید به توسعه یک مدل MLP بپردازیم که می تواند نگاشت ورودی ها را به خروجی ها بیاموزد.
مدل MLP
یک مدل ساده MLP دارای یک لایه پنهان از گره ها و یک لایه خروجی است که برای پیش بینی استفاده می شود.
ما می توانیم MLP را برای پیش بینی سری زمانی تک متغیره به شرح زیر تعریف کنیم.

در تعریف شکل ورودی مهم است. این همان چیزی است که مدل از نظر تعداد گام های زمانی، به عنوان ورودی برای هر نمونه انتظار دارد.
تعداد مراحل زمانی به عنوان ورودی، عددی است که هنگام تهیه مجموعه داده خود به عنوان آرگومان تابع split_sequence انتخاب کردیم.
بعد ورودی برای هر نمونه در آرگومان input_dim در مورد تعریف اولین لایه پنهان مشخص شده است. از نظر فنی، مدل به جای مراحل زمانی جداگانه، هر مرحله از زمان را به عنوان یک ویژگی جداگانه مشاهده می کند.
ما تقریباً همیشه چندین نمونه داریم، بنابراین، مدل انتظار دارد که م مولفه ورودی داده های آموزشی دارای ابعاد یا شکل باشد:

تابع split_sequence ما در بخش قبلی X را با شکلی [نمونه ها ، ویژگی ها] آماده برای استفاده برای مدل سازی، خروجی می دهد.
این مدل با استفاده از Adam version of stochastic gradient descent مناسب است و با استفاده از میانگین خطای مربع یا تابع ضرر MSE بهینه شده است.
پس از تعریف مدل، می توانیم آن را در مجموعه داده های آموزشی جای دهیم.

پس از فیت شدن مدل، می توانیم از آن برای پیش بینی استفاده کنیم.
با تهیه ورودی می توان مقدار بعدی را در توالی پیش بینی کرد:

و انتظار داریم که مدل چیزی مانند این را پیش بینی کند:

مدل انتظار دارد که شکل ورودی با [نمونه ها، ویژگی ها] دو بعدی باشد، بنابراین، ما باید قبل از پیش بینی نمونه ورودی تک را تغییر شکل دهیم، به عنوان مثال با شکل [1، 3] برای 1 نمونه و 3 مرحله زمان استفاده شده به عنوان ویژگی های ورودی.

ما می توانیم همه اینها را بهم گره بزنیم و نشان دهیم که چگونه می توان MLP را برای پیش بینی سری زمانی تک متغیره تهیه کرد و یک پیش بینی واحد انجام داد.
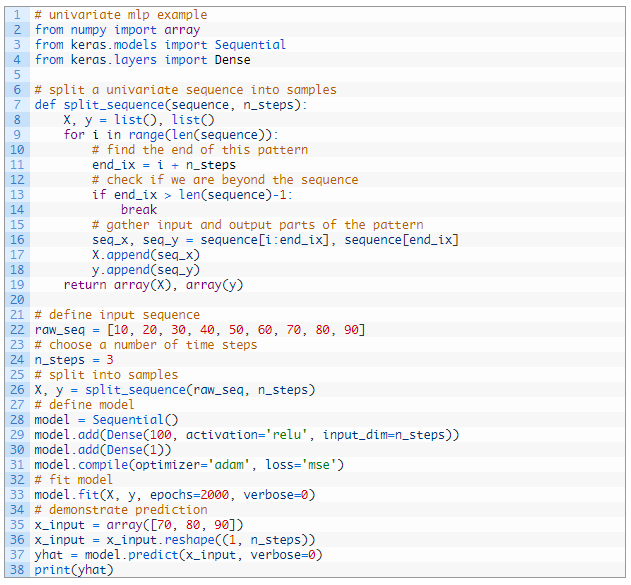
اجرای مثال داده ها را آماده می کند، با مدل فیت می شود و پیش بینی می کند.
توجه: نتایج شما ممکن است با توجه به ماهیت تصادفی الگوریتم یا روش ارزیابی، یا تفاوت در دقت عددی متفاوت باشد. چند بار اجرای مثال را در نظر بگیرید و نتیجه متوسط را مقایسه کنید.
می بینیم که مدل مقدار بعدی را در توالی پیش بینی می کند.
مدلهای چند متغیره MLP
داده های سری زمانی چند متغیره به معنی داده هایی است که برای هر مرحله زمانی بیش از یک مشاهده وجود دارد.
دو مدل اصلی وجود دارد که ممکن است با داده های سری زمانی چند متغیره به آنها نیاز داشته باشیم. آن ها عبارتند از:
- سری ورودی چندگانه - Multiple Input Series
- سری موازی چندگانه - Multiple Parallel Series
بیایید به نوبت به هر یک نگاهی بیندازیم.
سری ورودی چندگانه
یک مساله ممکن است دو یا چند سری زمانی ورودی موازی و یک سری زمانی خروجی داشته باشد که به سری زمانی ورودی وابسته باشد.
سری های زمانی ورودی موازی هستند زیرا هر سری در یک مرحله زمانی دارای یک مشاهده هستند.
ما می توانیم این را با یک مثال ساده از دو سری زمانی ورودی موازی نشان دهیم که در آن مجموعه خروجی جمع ساده سری ورودی است.

ما می توانیم این سه آرایه داده را به صورت یک مجموعه داده واحد تغییر شکل دهیم که در آن هر سطر یک مرحله زمانی است و هر ستون یک سری زمانی جداگانه است. این یک روش استاندارد برای ذخیره سری های زمانی موازی در یک فایل CSV است.

مثال کامل در زیر ذکر شده است.
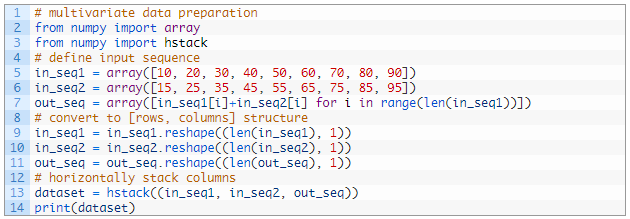
با اجرای مثال، مجموعه داده با یک ردیف در هر مرحله زمان و یک ستون برای هر دو سری ورودی موازی و یک خروجی چاپ می شود.
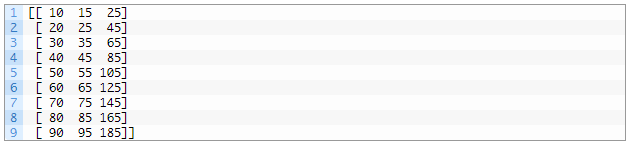
همانند سری زمانی تک متغیره، ما باید این داده ها را در مثال هایی با نمونه های ورودی و خروجی ساختار دهیم.
ما باید داده ها را با حفظ ترتیب مشاهدات در دو توالی ورودی به نمونه تقسیم کنیم.
اگر سه مرحله زمان ورودی را انتخاب کنیم، اولین نمونه به صورت زیر است:
ورودی:

خروجی:

یعنی سه مرحله زمانی اول از هر سری موازی به عنوان ورودی به مدل ارائه می شود و مدل این را با مقدار سری خروجی در مرحله زمان سوم مرتبط می کند، در این مورد 65.
می توانیم ببینیم که، در تبدیل سری های زمانی به نمونه های ورودی / خروجی برای آموزش مدل، مجبور خواهیم بود برخی مقادیر را از سری زمانی خروجی که در مراحل زمانی قبلی مقادیری در سری زمان ورودی نداریم، کنار بگذاریم. به نوبه خود، انتخاب اندازه تعداد گام های زمان ورودی تأثیر مهمی در میزان استفاده از داده های آموزش خواهد داشت.
ما می توانیم تابعی به نام split_sequences تعریف کنیم که یک مجموعه داده را بگیرد همانطور که ما آن را با سطرهایی برای مراحل زمان و ستون ها برای سری های موازی تعریف کرده و نمونه های ورودی / خروجی را برگردانده ایم.

ما می توانیم این تابع را با استفاده از سه مرحله زمانی برای هر سری زمانی ورودی به عنوان ورودی، روی مجموعه داده خود آزمایش کنیم.
مثال کامل در زیر ذکر شده است:
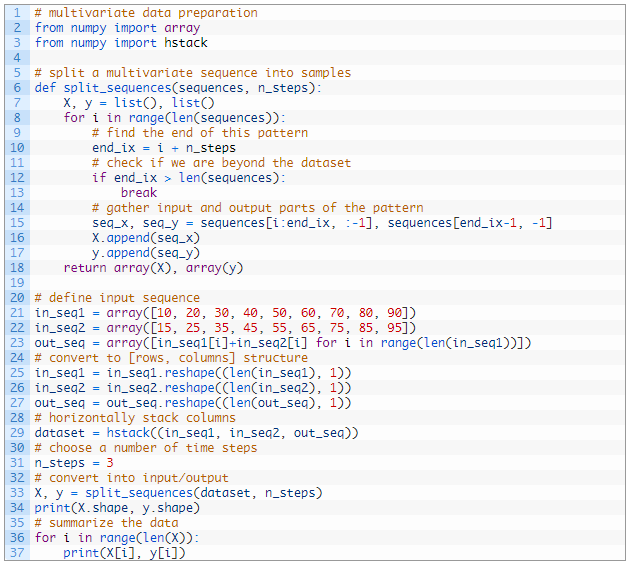
اجرای مثال ابتدا شکل اجزای X و y را چاپ می کند.
می توانیم ببینیم که مولفه X ساختاری سه بعدی دارد.
بعد اول تعداد نمونه ها است، در این حالت 7. بعد دوم تعداد مراحل زمانی در هر نمونه است، در این حالت 3، مقدار مشخص شده برای تابع. سرانجام، آخرین بعد تعداد سری های زمانی موازی یا تعداد متغیرها را مشخص می کند، در اینجا 2 مورد برای دو سری موازی.
سپس می توانیم ببینیم که ورودی و خروجی برای هر نمونه چاپ شده است، سه مرحله زمانی برای هر یک از دو سری ورودی و خروجی مربوط به هر نمونه را نشان می دهد.

قبل از اینکه بتوانیم MLP را روی این داده ها جا دهیم، باید شکل نمونه های ورودی را صاف کنیم.
MLP ها نیاز دارند که شکل قسمت ورودی هر نمونه یک بردار باشد. با یک ورودی چند متغیره، ما چندین بردار خواهیم داشت، یکی برای هر مرحله زمان.
ما می توانیم ساختار زمانی هر نمونه ورودی را صاف کنیم، بنابراین:

تبدیل می شود:

ابتدا می توانیم طول هر بردار ورودی را به صورت تعداد مراحل زمانی ضرب در تعداد ویژگی ها یا سری های زمانی محاسبه کنیم. سپس می توانیم از این اندازه برداری برای تغییر شکل ورودی استفاده کنیم.

اکنون می توانیم یک مدل MLP برای ورودی چند متغیره تعریف کنیم که در آن از طول بردار برای آرگومان بعد ورودی استفاده می شود.

هنگام پیش بینی، مدل انتظار می رود سه مرحله زمان برای دو سری زمانی ورودی داشته باشد.
ما می توانیم مقدار بعدی را در سری خروجی ثابت کنیم که مقادیر ورودی را اثبات می کند:

شکل 1 نمونه با 3 مرحله زمانی و 2 متغیر [1، 3، 2] خواهد بود. ما باید دوباره این را به شکل 1 نمونه با بردار 6 عنصر یا [1، 6] درآوریم
انتظار داریم مقدار بعدی در دنباله 100 + 105 یا 205 باشد.

مثال کامل در زیر ذکر شده است.
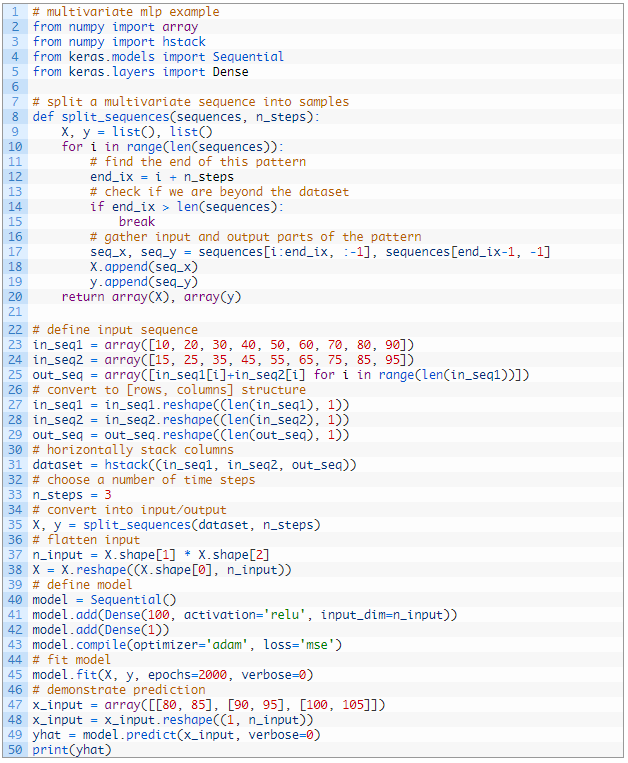
توجه: نتایج شما ممکن است با توجه به ماهیت تصادفی الگوریتم یا روش ارزیابی، یا تفاوت در دقت عددی متفاوت باشد. چند بار اجرای مثال را در نظر بگیرید و نتیجه متوسط را مقایسه کنید.
اجرای مثال داده ها را آماده می کند، مدل فیت شده و پیش بینی می کند.

روش مفصل دیگری نیز برای مدل سازی مسئله وجود دارد.
هر سری ورودی را می توان با MLP جداگانه اداره کرد و می توان خروجی هر یک از این زیرمدل ها را قبل از پیش بینی برای توالی خروجی ترکیب کرد.
می توانیم از این به عنوان یک مدل MLP ورودی چند سر استفاده کنیم. بسته به مشخصات مسئله ای که در حال مدل سازی است، ممکن است انعطاف پذیری بیشتر یا عملکرد بهتری داشته باشد.
این نوع مدل را می توان در Keras با استفاده از API کاربردی Keras تعریف کرد.
ابتدا می توان اولین مدل ورودی را MLP با یک لایه ورودی تعریف کرد که انتظار بردارهایی با ویژگی های n_steps را دارد.

ما می توانیم زیرمدل ورودی دوم را نیز به همین ترتیب تعریف کنیم.

اکنون که هر دو زیرمدل ورودی تعریف شده اند، می توانیم خروجی از هر مدل را در یک بردار طولانی ادغام کنیم، که می تواند قبل از پیش بینی توالی خروجی تفسیر شود.

سپس می توانیم ورودی ها و خروجی ها را بهم گره بزنیم.
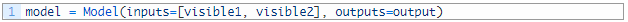
تصویر زیر شماتیک برای نحوه به نظر رسیدن این مدل شامل شکل ورودی و خروجی هر لایه را ارائه می دهد.
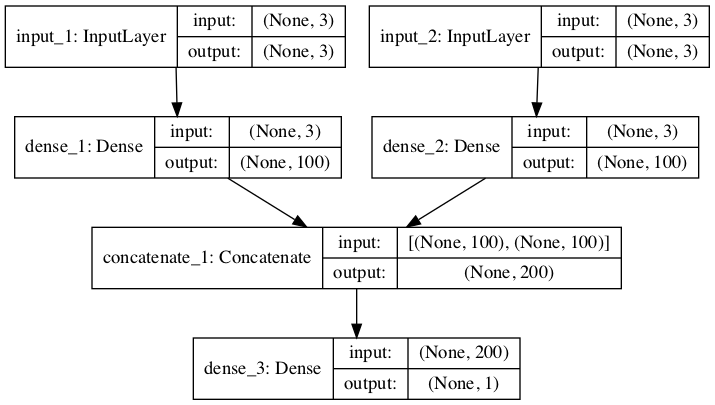
نمودار MLP چند هد برای پیش بینی سری زمانی چند متغیره
این مدل نیاز دارد ورودی به عنوان لیستی از دو عنصر ارائه شود، جایی که هر عنصر در لیست حاوی داده های یکی از زیر مدل ها است.
برای دستیابی به این هدف، می توانیم داده های ورودی سه بعدی را به دو آرایه جداگانه از داده های ورودی تقسیم کنیم: این از یک آرایه با شکل [7، 3، 2] تا دو آرایه 2D با شکل [7، 3] است

سپس می توان این داده ها را متناسب با مدل ارائه داد.

به همین ترتیب، هنگام انجام پیش بینی یک مرحله ای، باید داده ها را برای یک نمونه واحد به عنوان دو آرایه جداگانه دو بعدی آماده کنیم.

ما می توانیم همه اینها را به هم گره بزنیم. مثال کامل در زیر ذکر شده است.
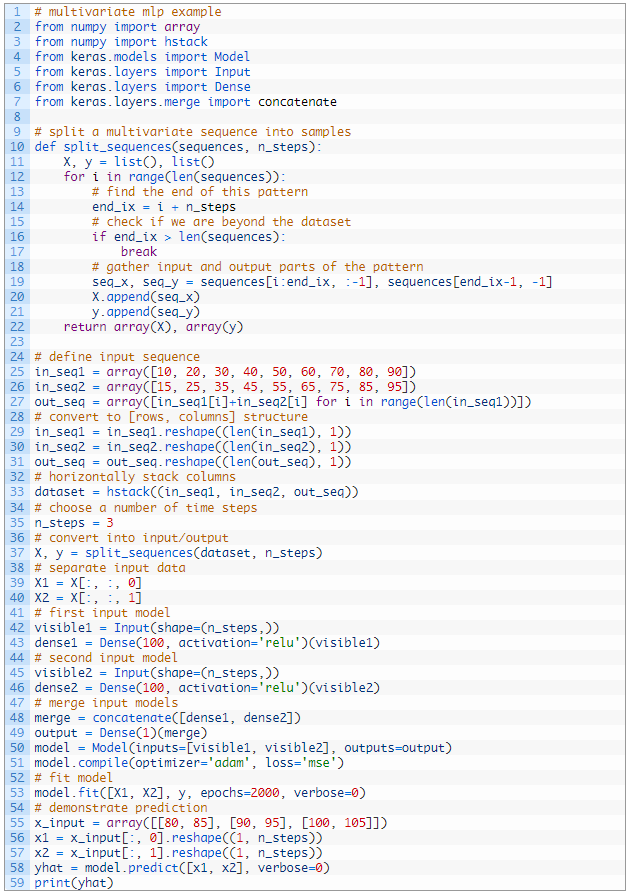
توجه: نتایج شما ممکن است با توجه به ماهیت تصادفی الگوریتم یا روش ارزیابی، یا تفاوت در دقت عددی متفاوت باشد. چند بار اجرای مثال را در نظر بگیرید و نتیجه متوسط را مقایسه کنید.
اجرای مثال داده ها را آماده می کند، متناسب با مدل است و پیش بینی می کند.



مدیر سایت: بهزاد سرهادی کارشناس ارشد مهندسی آب
شناسه تلگرام مدیر سایت: SubBasin@
نشانی ایمیل: behzadsarhadi@gmail.com
(سوالات تخصصی را در گروه تلگرام ارسال کنید)
_______________________________________________________
پروژه تخصصی در لینکدین









 در منابع آب
در منابع آب





































نظرات (۰)