11 روش کلاسیک پیش بینی سری زمانی در پایتون - بخش اول

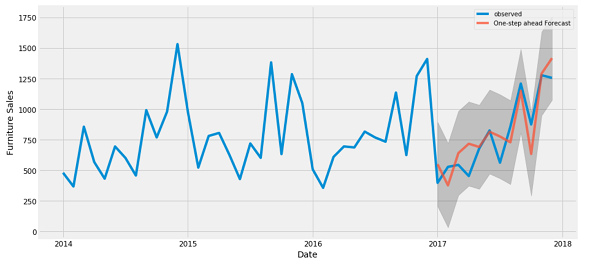
۲۴ آبان ۹۹ ، ۱۲:۴۸ نويسنده: بهزاد سرهادی

از روش های یادگیری ماشین می توان برای طبقه بندی و پیش بینی مسائل سری زمانی استفاده کرد. قبل از کاوش در روشهای یادگیری ماشین برای سری های زمانی، بهتر است اطمینان حاصل کنید که آموزش روشهای پیش بینی سری زمانی خطی کلاسیک را به اتمام رسانده اید. روش های کلاسیک پیش بینی سری زمانی ممکن است بر روی روابط خطی متمرکز شده باشند، با این وجود، این روش ها پیچیده هستند و در طیف گسترده ای از مسائل عملکرد خوبی دارند، با این فرض که داده های شما به درستی آماده شده و روش به خوبی پیکربندی شده است.

در این پست، مجموعه ای از روش های کلاسیک برای پیش بینی سری های زمانی را می یابید که می توانید قبل از کاوش در روش های یادگیری ماشین، مساله پیش بینی خود را آزمایش کنید.

ساختار این پست به صورتی ساخته شده است تا اطلاعات کافی در مورد هر روش را در اختیار شما قرار دهد تا با یک مثال کد کار شروع کنید و جستجو کنید تا اطلاعات بیشتری در مورد روش کسب کنید. همه مثال ها در کد پایتون هستند و از کتابخانه Statsmodels استفاده می کنند. API های این کتابخانه برای مبتدیان مشکل است، بنابراین داشتن یک مثال کد کار به عنوان نقطه شروع پیشرفت شما را بسیار تسریع می کند.

بررسی اجمالی

این صفحه 11 روش مختلف پیش بینی سری زمانی کلاسیک را نشان می دهد. آن ها عبارت هستند از:

Autoregression (AR)
Moving Average (MA)
Autoregressive Moving Average (ARMA)
Autoregressive Integrated Moving Average (ARIMA)
Seasonal Autoregressive Integrated Moving-Average (SARIMA)
Seasonal Autoregressive Integrated Moving-Average with Exogenous Regressors (SARIMAX)
Vector Autoregression (VAR)
Vector Autoregression Moving-Average (VARMA)
Vector Autoregression Moving-Average with Exogenous Regressors (VARMAX)
Simple Exponential Smoothing (SES)
Holt Winter’s Exponential Smoothing (HWES)

هر روش به صورتی ثابت ارائه می شود. این شامل:

شرح. شرح مختصر و تکنیک دقیق.
کد پایتون یک نمونه کار کوتاه متناسب با مدل و پیش بینی در پایتون است.
اطلاعات بیشتر. منابع برای API و الگوریتم.

هر مثال کد در یک مجموعه داده ساده ساختاری نشان داده شده است که ممکن است برای این روش مناسب باشد یا نباشد. برای آزمایش روش، داده خود را با داده های مثال جایگزین کنید.

به یاد داشته باشید: هر روش نیاز به تنظیم مساله خاص شما دارد. در بسیاری از موارد، من نمونه هایی از نحوه پیکربندی و حتی شبکه کردن پارامترهای جستجو را در سایت دارم، و عملکرد جستجو را امتحان می کنم.

Autoregression-AR

روش خود همبستگی مرحله بعدی توالی را به عنوان یک تابع خطی از مشاهدات در مراحل زمان قبلی، را مدل می کند.

علامت گذاری برای مدل شامل تعیین ترتیب مدل p به عنوان یک پارامتر برای تابع AR است، به عنوان مثال AR p و عنوان مثال، AR 1 یک مدل خود رگرسیون مرتبه اول است.

این روش برای سری های زمانی تک متغیره بدون روند و مولفه های فصلی مناسب است.

کد پایتون

# AR example

from statsmodels.tsa.ar_model import AutoReg

from random import random

# contrived dataset

data = [x + random() for x in range(1, 100)]

# fit model

model = AutoReg(data, lags=1)

model_fit = model.fit()

# make prediction

yhat = model_fit.predict(len(data), len(data))

print(yhat)

اطلاعات بیشتر

statsmodels.tsa.ar_model.AutoReg API

statsmodels.tsa.ar_model.AutoRegResults API

مدل خود همبستگی در ویکی پدیا

Moving Average-MA

روش میانگین متحرک (MA) مرحله بعدی توالی را به عنوان یک تابع خطی از خطاهای باقیمانده از یک فرآیند میانگین در مراحل زمان قبلی، مدل می کند.

مدل میانگین متحرک با محاسبه میانگین متحرک سری های زمانی متفاوت است.

علامت گذاری برای مدل شامل تعیین ترتیب مدل q به عنوان یک پارامتر برای عملکرد MA است، به عنوان مثال. MA q و به عنوان مثال، MA 1 یک مدل میانگین متحرک مرتبه اول است.

این روش برای سری های زمانی تک متغیره بدون روند و مولفه های فصلی مناسب است.

کد پایتون

ما می توانیم از کلاس ARMA برای ایجاد یک مدل MA و تنظیم یک مدل AR با ترتیب صفر استفاده کنیم. ما باید ترتیب مدل MA را در آرگومان ترتیب مشخص کنیم.

# MA example

from statsmodels.tsa.arima.model import ARIMA

from random import random

# contrived dataset

data = [x + random() for x in range(1, 100)]

# fit model

model = ARIMA(data, order=(0, 0, 1))

model_fit = model.fit()

# make prediction

yhat = model_fit.predict(len(data), len(data))

print(yhat)

اطلاعات بیشتر

statsmodels.tsa.arima_model.ARMA API

statsmodels.tsa.arima_model.ARMAResults API

میانگین متحرک در ویکی پدیا

میانگین متحرک خود همبسته (ARMA)

روش میانگین متحرک خود همبسته (ARMA) مرحله بعدی توالی را به عنوان یک تابع خطی از مشاهدات و خطاهای resiudal در مراحل زمان قبلی، مدل می کند.

این روش هر دو مدل Autoregression-AR و Moving Average-MA را ترکیب می کند.

علامت گذاری برای مدل شامل تعیین ترتیب برای مدل های AR p و MA q به عنوان پارامترهای یک عملکرد ARMA است، به عنوان مثال. ARMA p، q. برای توسعه مدل های AR یا MA می توان از یک مدل ARIMA استفاده کرد.

این روش برای سری های زمانی تک متغیره بدون روند و مولفه های فصلی مناسب است.

کد پایتون

# ARMA example

from statsmodels.tsa.arima.model import ARIMA

from random import random

# contrived dataset

data = [random() for x in range(1, 100)]

# fit model

model = ARIMA(data, order=(2, 0, 1))

model_fit = model.fit()

# make prediction

yhat = model_fit.predict(len(data), len(data))

print(yhat)

اطلاعات بیشتر

statsmodels.tsa.arima_model.ARMA API

statsmodels.tsa.arima_model.ARMAResults API

خود همبستگی - میانگین متحرک در ویکی پدیا

Autoregressive Integrated Moving Average-ARIMA

روش میانگین متحرک خود همبسته یکپارچه (ARIMA) مرحله بعدی توالی را به عنوان یک تابع خطی از تفاضل مشاهدات و خطاهای residual در مراحل زمان قبلی، را مدل می کند.

این هر دو مدل Autoregression-AR و Moving Average-MA و همچنین یک مرحله تفکیک مرحله قبل از پردازش توالی را ترکیب می کند تا توالی ثابت شود ، به اصطلاح یکپارچه شود (I).

علامت گذاری برای مدل شامل تعیین ترتیب برای مدل های AR p ،I d و MA q به عنوان پارامترهای یک تابع ARIMA است، به عنوان مثال. ARIMA p ،d ،q. برای توسعه مدل های AR ،MA و ARMA می توان از یک مدل ARIMA نیز استفاده کرد.

این روش برای سری های زمانی تک متغیره با روند و بدون مولفه های فصلی مناسب است.

کد پایتون

# ARIMA example

from statsmodels.tsa.arima.model import ARIMA

from random import random

# contrived dataset

data = [x + random() for x in range(1, 100)]

# fit model

model = ARIMA(data, order=(1, 1, 1))

model_fit = model.fit()

# make prediction

yhat = model_fit.predict(len(data), len(data), typ='levels')

print(yhat)

اطلاعات بیشتر

statsmodels.tsa.arima_model.ARIMA API

statsmodels.tsa.arima_model.ARIMAResults API

میانگین متحرک خود همبستگی در ویکی پدیا

Seasonal Autoregressive Integrated Moving-Average-SARIMA

میانگین متحرک خود همبسته فصلی (SARIMA) مرحله بعدی توالی را به عنوان یک تابع خطی از مشاهدات متفاوت، خطاها، مشاهدات فصلی متفاوت و خطاهای فصلی در مراحل زمان قبلی، مدل می کند.

این مدل ARIMA را با توانایی انجام مدل رگرسیون خودکار، متفاوت سازی و حرکت میانگین در سطح فصلی ترکیب می کند.

علامت گذاری برای مدل شامل تعیین ترتیب برای مدل های AR(p) ، I(d) و MA(q) به عنوان پارامترهای یک تابع ARIMA و AR(P) ، I(D) ، MA (Q) و m است پارامترها در سطح فصلی، به عنوان مثال SARIMA (p ،d ،q) (P ،D ،Q)m که "m" تعداد مراحل زمانی در هر فصل است (دوره فصلی). از مدل SARIMA می توان برای توسعه مدل های AR ،MA ،ARMA و ARIMA استفاده کرد.

این روش برای سری های زمانی تک متغیره با روند و / یا مولفه های فصلی مناسب است.

کد پایتون

# SARIMA example

from statsmodels.tsa.statespace.sarimax import SARIMAX

from random import random

# contrived dataset

data = [x + random() for x in range(1, 100)]

# fit model

model = SARIMAX(data, order=(1, 1, 1), seasonal_order=(0, 0, 0, 0))

model_fit = model.fit(disp=False)

# make prediction

yhat = model_fit.predict(len(data), len(data))

print(yhat)

اطلاعات بیشتر

statsmodels.tsa.statespace.sarimax.SARIMAX API

statsmodels.tsa.statespace.sarimax.SARIMAXResults API

میانگین متحرک خود همبستگی در ویکی پدیا

Seasonal Autoregressive Integrated Moving-Average with Exogenous Regressors (SARIMAX)

میانگین متحرک خود همبسته فصلی با رگرسورهای برون زا (SARIMAX) پسوند مدل SARIMA است که شامل مدل سازی متغیرهای برون زا نیز می باشد.

متغیرهای برون متغیر نیز نامیده می شوند و می توان آنها را به عنوان توالی ورودی موازی در نظر گرفت که دارای مشاهدات در همان مراحل زمانی با سری اصلی هستند. از سری اولیه می توان به عنوان داده های درون زا یاد کرد تا آن را از توالی (های) برون زا متضاد کند. مشاهدات مربوط به متغیرهای برونزا در هر مرحله به طور مستقیم در مدل گنجانده می شود و به همان روشی که توالی درون زای اولیه (به عنوان مثال به عنوان فرایند AR ،MA و غیره) مدلسازی نمی شود.

از روش SARIMAX همچنین می توان برای مدل سازی مدل های فرعی با متغیرهای برونزا، مانند ARX ،MAX ،ARMAX و ARIMAX استفاده کرد.

این روش برای سری های زمانی تک متغیره با روند و / یا مولفه های فصلی و متغیرهای برون زای مناسب است.

کد پایتون

# SARIMAX example

from statsmodels.tsa.statespace.sarimax import SARIMAX

from random import random

# contrived dataset

data1 = [x + random() for x in range(1, 100)]

data2 = [x + random() for x in range(101, 200)]

# fit model

model = SARIMAX(data1, exog=data2, order=(1, 1, 1), seasonal_order=(0, 0, 0, 0))

model_fit = model.fit(disp=False)

# make prediction

exog2 = [200 + random()]

yhat = model_fit.predict(len(data1), len(data1), exog=[exog2])

print(yhat)

اطلاعات بیشتر

statsmodels.tsa.statespace.sarimax.SARIMAX API

statsmodels.tsa.statespace.sarimax.SARIMAXResults API

میانگین متحرک خود همبسته در ویکی پدیا

دسترسی به عناوین دیگر محتوای مرتبط با این بخش

مدیر سایت: بهزاد سرهادی

شماره تلفن: 09190622992

شناسه تلگرام مدیر سایت: SubBasin@

نشانی ایمیل: behzadsarhadi@gmail.com

(سوالات تخصصی را در گروه تلگرام ارسال کنید)

_______________________________________________________

پروژه تخصصی در لینکدین

براي پيوستن به بزرگترين گروه تلگرام علوم و مهندسي آب با امکان تبادل نظر بين اعضاء کليک کنيد

کتاب کاربرد مدل QUAL2KW

کتاب کاربرد GIS در منابع آب

کتاب محاسبه سيل طرح

نظرات (۰)

هيچ نظري هنوز ثبت نشده است

فرم ارسال نظر

ارسال نظر آزاد است، اما اگر قبلا در بیان ثبت نام کرده اید می توانید ابتدا وارد شوید.

نام *

پست الکترونيک

سایت یا وبلاگ

پیام *

شما میتوانید از این تگهای html استفاده کنید:

یا ، یا ، ، <strike> یا <s>، ، ، <blockquote>، <code>، <pre>، <hr>، ، ، <a href="" title="">، ، <div align="">

کد امنیتی *

ارقام فارسی و انگلیسی پذیرفته می‌شوند

نظر بصورت خصوصی ارسال شود

پست الکترونیک برای عموم قابل مشاهده باشد

ويدئوهاي آموزش جامع نرم افزار HEC-HMS - مدل بارش رواناب

ويدئو مدلسازي کمي جريان آب زيرزميني با SEAWAT- GMS

پروژه جامع هيدرولوژي-آناليز منطقه اي، فيزيوگرافي، مدل بارش-رواناب

کتاب تحلیل مدل های تعادلی و ارائه مدل ایزوترم جذب

آموزش مدل سازی سیل با Aquaveo SMS - TUFLOW + کتاب

پروژه تخلیه آب زیرسطحی از فونداسیون یک برج

درباره بهترين هاي بيسيـــن بدانيد...

يکي از مهمترين اهداف اين سايت تهيه آموزش هاي روان از ابزارهاي کاربردي علوم آب است.

اهميت مطالعات محيطي با ابزارهاي نوين در چيست؟

امروز با فارغ التحصيلي جمع کثير دانشجويان سالهاي گذشته و حال، با گذر از کمي گرايي ديگر صرف وجود مدارک دانشگاهي حرف اول را در بازار کار نمي زند؛ بلکه سنجش ديگري ملاک؛ و شايسته سالاري به ناچار! باب خواهد شد. يکي از مهم ترين لوازم توسعه علمي در هر کشور و ارائه موضوعات ابتکاري، بهره گيري از ابزار نوين است، بيسين با همکاري مخاطبان مي تواند در حيطه علوم آب به معرفي اين مهم بپردازد.

جستجو در بيسين