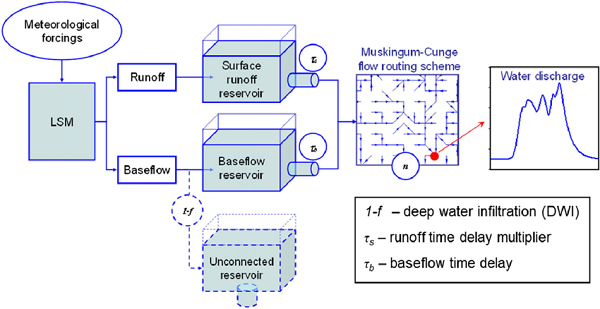
1.5 مسیریابی یا روندیابی رودخانه

در چرخه طبیعی آب می توان سه عامل اصلی هیدرولوژیک را شناسایی کرد (شکل 1.5):

• عملکرد تولید، مورد استفاده برای جداسازی کل بارندگی و بارندگی موثر؛
• عملکرد انتقال، تبدیل بارندگی موثر در تخلیه رودخانه؛
• عملکرد مسیریابی، در مورد تبدیل جریان در امتداد رودخانه ها.

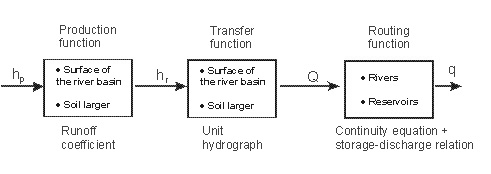
شکل 1.5 اپراتورهای اصلی چرخه هیدرولوژیک.

در هنگام طغیان، دو روند اصلی در امتداد رودخانه رخ می دهد:

- ترکیب امواج سیل در نقاط تلاقی؛ در هر لحظه t، تخلیه رودخانه اصلی و سرشاخه خلاصه می شود، بنابراین تخلیه کل پایین دست تلاقی جریان (شکل 2.5):

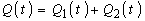
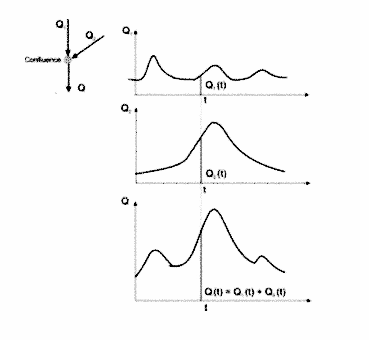
شکل 2.5 محاسبه تخلیه در پایین دست یک محل تلاقی.

- انتشار سیل در رودخانه. سیل پایین دست به ندرت تبدیل می شود (شکل 3.5 الف). در بیشتر موارد، در انتهای پایین دست یک هیدروگراف حاصل از هیدروگراف ورودی متفاوت است و توزیع مجدد می شود (شکل 3.5 ب).

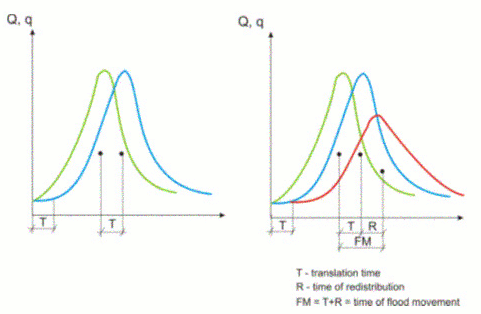
شکل 3.5 انتشار سیل.

در تپه یا در مناطق دشت، بستر رودخانه به خوبی توسعه یافته است. در آنجا، ضریب زبری بسیار بیشتر از بستر کوچک رودخانه است. در نتیجه حرکت آب در چمنزار رودخانه کندتر از قسمت مرکزی است. بنابراین، هیدروگراف پایین دستی در معرض یک فرآیند میرایی طبیعی قرار می گیرد (شکل 3.5 ب)، صاف شده و با جابجایی مرکز میانه روبرو می شود.

وقتی مخزنی با سرریز غیرقابل کنترل دارای سطح آب افقی باشد، اوج تخلیه خروجی لزوماً روی بخش در حال کاهش هیدروگراف ورودی قرار دارد. برای رسیدن به رودخانه، موقعیت اوج تخلیه خروجی نه تنها به طول رسیدن رودخانه بلکه به برخی از مشخصات هیدرولیکی مانند شیب بستر و ضرایب زبری بستگی دارد.

فاصله زمانی بین سانتروئیدهای هیدروگراف ورودی و هیدروگراف خروجی، که تقریباً با فاصله زمانی بین دو قله برابر است، تقریباً بیانگر زمان انتشار در محدوده مشاهده شده است. هرچه دسترسی بیشتر باشد، فاصله زمانی بیشتر است.

مسیریابی سیل یک روش ریاضی برای پیش بینی میزان تغییر شکل و شکل یک موج سیل در یک یا چند نقطه از یک رودخانه با استفاده از هیدروگراف های شناخته شده یا فرض شده در یک یا چند نقطه بالادست است (Chow و همکاران، 1988، و Maidment، 1993). اگر جریان به آبهای متوسط ​​یا کم وجود دارد، می توان از همان روش ها استفاده کرد، اما معمولاً به عنوان مسیر یابی جریان شناخته می شوند.

مسیر یابی سیل را می توان با استفاده از مدل های هیدرولوژیکی مانند Muskingum، Kalinin-Miljukov و غیره، یا مدل های هیدرولیکی بر اساس سیستم شناخته شده معادلات Saint-Vénant انجام داد. در هر دو مورد، هیدروگراف ورودی در انتهای بالادست حد مشاهده می شود. مسیریابی هیدرولوژیکی، معروف به مسیریابی توده ای، مستقیماً امکان محاسبه هیدروگراف خروجی در انتهای پایین دست را فراهم می کند (شکل 5.4 الف). فقط به دو پارامتر نیاز است. مسیریابی هیدرولیکی، شناخته شده به عنوان مسیریابی توزیع شده، نیاز به محاسبه دبی در امتداد رودخانه در تعداد مهمی از نقاط میانی، برای هر مرحله دارد (شکل 4.5 ب). در کنار مقاطع عرضی در این نقاط میانی، پارامترهای هیدرولیکی مورد نیاز است (حداقل دو ضریب زبری، یکی برای بستر جزئی و دیگری برای بستر اصلی).

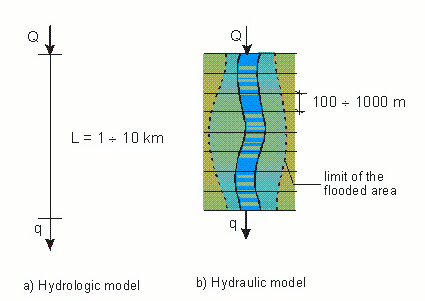
شکل 4.5 اصول اساسی مسیریابی سیل.

مدل های هیدرولوژیک منجر به نتایج تقریبی می شوند، اما به دلیل اینکه آنها به داده های کمتری نیاز دارند و سریعاً نتایج را ارائه می دهند، هنوز هم در عمل فعلی تا حد زیادی مورد استفاده قرار می گیرند.

1.1.5 فرم گسسته شده مدل Muskingum

الف) مدل ریاضی

بگذارید یک رودخانه را در نظر بگیریم، جایی که هیدروگراف ورودی Q و هیدروگراف خروجی q مشخص هستند (شکل 5.5).

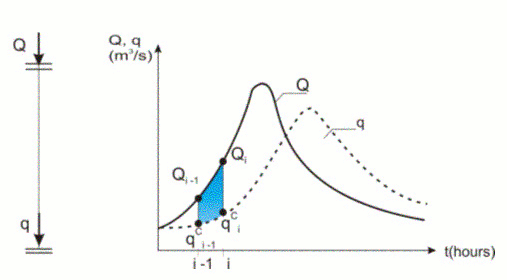
شکل 5.5 تغییر فضای ذخیره سازی در فاصله زمانی t.

اصل حفظ جرم مستلزم تفاوت بین دو جریان با تغییر زمان ذخیره است:

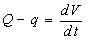
پس از گسسته سازی، معادله (2) می شود:

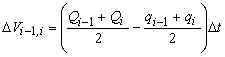
با محاسبه میزان ذخیره در رودخانه بین مراحل زمانی i-1 و i. اولین اصطلاح براکت میانگین جریان را نشان می دهد، در حالی که دومین میانگین خروجی در فاصله زمانی Δt است.

معادله تداوم برای یافتن راه حل کافی نیست زیرا دو ناشناخته وجود دارد: ذخیره سازی V و جریان خروجی q. رابطه دیگر با عملکرد تجربی ذخیره سازی نشان داده می شود (شکل 6.5).

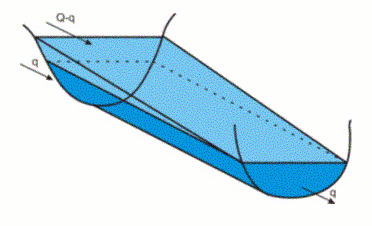
شکل 6.5 نمایش ساده ذخیره سازی در رودخانه.

ذخیره در رودخانه در مرحله زمانی i ترکیبی از یک بخش منشوری در قسمت پایین و یک ذخیره گوه ای در قسمت بالایی است. تخلیه ورودی را می توان مجموع دو جز دانست:

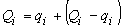
ذخیره منشوری، به دلیل تخلیه q، برابر است با:

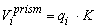
جایی که K در واحد زمان بیان می شود (معمولاً ساعت) و نشان دهنده زمان مورد نیاز برای تخلیه q از بالادست به سطح مقطع پایین دست دسترسی است.

ذخیره گوه ای با استفاده از یک رابطه مشابه به دست می آید. هنوز، چون تخلیه متناظر در امتداد رسیدن از Q-q (بالادست) به صفر (پایین دست) متغیر است، بنابراین باید از یک مقدار متوسط بین این دو مقدار شدید استفاده کرد. اگر سطح آب یک صفحه باشد، می توان از تخلیه متوسط در دسترس استفاده کرد:

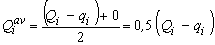
در واقع، سطح آب یک صفحه نیست و ضریب کاهش مربوط به ذخیره گوه ای بین 0 (به معنای ذخیره کل اختلاف Q_i-q_i در یک مخزن) و 0.5 همانطور که قبلا نشان داده شد (سطج آب صفحه ای) متغیر است.

به عبارت دیگر، مقدار متوسط ​​تخلیه مربوط به ذخیره گوه ای را می توان به صورت زیر نوشت:

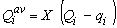
همانطور که نشان داده شد، X یک عامل وزنی بین 0 تا 0.5 است:

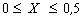
با در نظر گرفتن مجدد K به عنوان زمان انتشار بین دو انتهای محل دسترسی، ذخیره گوه ای را می توان به صورت زیر بیان کرد:

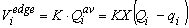
بنابراین کل ذخیره موجود در لحظه t = iΔt مجموع دو مولفه است:

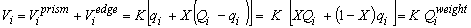
که در آن Q_i^weight تخلیه واسطه ای بین Q و q است. در واقع، ذخیره سازی به طور خطی با Q و q مرتبط است.

با جایگزینی شاخص i با i-1، ذخیره در لحظه t = i.Δt بدست می آید:

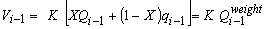
از این رو، ذخیره محل دسترسی بین دو مرحله زمانی پی در پی خواهد بود:

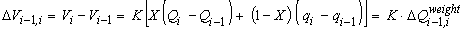
از معادلات حاضر به شرح زیر نتیجه می شود:

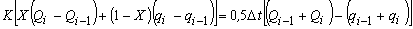
با گروه بندی اصطلاحات، تخلیه q_i پایین دست را می توان به عنوان یک تابع خطی تخلیه Q_i, Q_i-1 و q_i-1 بیان کرد (شکل 7.5):

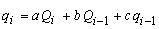
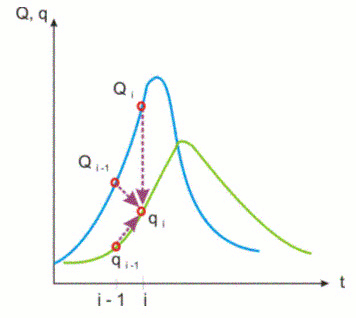
شکل 7.5 محاسبه تخلیه پایین دست.

ضرایب a، b و c عبارات زیر را دارند:

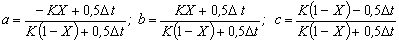
معادله حاضر به عنوان مدل ماسکینگام یا معادله انتشار در مدل ماسکینگام شناخته می شود. توجه داشته باشید که در این مدل مجموع ضرایب برابر با واحد است:

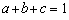
اگر محدودیت های غیر منفی ضرایب اضافه شود:

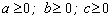
سپس رابطه اساسی از دیدگاه ریاضی، بیان q_i را به عنوان یک ترکیب خطی محدب از Q_i, Q_i-1 و q_i-1 نشان می دهد.

معادله مقادیر واحد میزان ذخیره سازی را بیان می کند، به این معنی که ذخیره سازی وارد شده در انتهای بالادست ورودی، انتهای پایین دست را ترک می کند. در حقیقت، بخشی از آب به بستر اصلی رودخانه نفوذ می کند یا در فرورفتگی های چمنزار رودخانه مسدود می شود. در نتیجه:

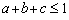
روابط در بالا منجر به عبارات زیر برای K و X می شود:

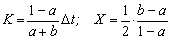
پارامترهای مدل را می توان پارامترهای K و X، که معنای فیزیکی دارند، یا پارامترهای مربوط به a، b و c، توابع K و X، اما فقط با یک تفسیر ریاضی در نظر گرفت.

ب) شرایط پایداری مدل Muskingum.

با در نظر گرفتن روابط و محدودیتهای بعدی، از این امر نتیجه می شود:

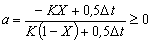
از آنجا که X ≤ 0.5، مخرج مثبت است و بنابراین:

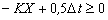
یا

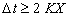
به روشی مشابه، شرط c ≥ 0 چنین اقتضا می کند:

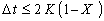
محدودیت های حاضر را می توان در یک محدودیت به صورت زیر بیان کرد:

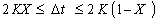
شرایط Courant  مستلزم آن است که مرحله زمان Δt باید کمتر از زمان موج سیل باشد تا فاصله بین دو انتهای رسیدن مشاهده شده را پوشش دهد. این زمان تقریباً برابر با K است، بنابراین می توان نوشت:

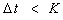
اگر این محدودیت نقض شود، ثبات عددی به خطر می افتد و در اولین مراحل محاسبه، می توان مقادیر منفی برای تخلیه های پایین دست بدست آورد.

محدودیت های موجود بیان می کنند که Δt باید به طور همزمان کمتر از K، به ترتیب 2K (1 - X) باشد.

از آنجا که X ≤ 0.5 نتیجه این است که 2 (1-X) ≥ 1، یا:

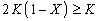
محدودیت های بالا را می توان به شکل زیر جمع کرد:

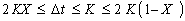
یا:

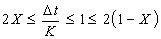
محدودیت های حاضر دامنه اعتبار پارامترهای مدل Muskingum را تعریف می کنند (Musy, 1998) (شکل 8.5). از آنجا که آخرین اصطلاح معادله معمولاً بزرگتر از عبارت قبلی است، حدود موثر نسبت Δt / K عبارتند از:

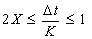
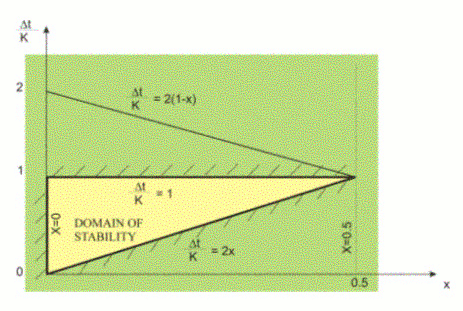
شکل 8.5 شرایط پایداری مدل Muskingum.

ج) انتشار در مسافتهای طولانی.

می توان دریافت که هرچه Δt به K نزدیکتر باشد، نوار اعتبار پارامترها بزرگتر است. معمولاً (Maidment و همکاران، 1993):

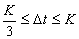
از طرف دیگر، گام زمان Δt برای تقریبی و حتی الامکان افزایش بخش هیدروگراف انتخاب شده است:

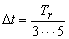
جایی که T_r زمان بالا آمدن هیدروگراف است.

استفاده از مقادیر کوچک برای Δt منجر به تقریب بهتر هیدروگراف می شود، اما به ویژه برای مقادیر بزرگتر X، ممکن است محدودیت معادله نقض شود. در نتیجه، ضریب a از رابطه انتشار منفی خواهد بود و تخلیه های محاسبه شده در مراحل اول نیز منفی خواهد بود.

به منظور ورود مجدد به حوزه پایداری، یا به عبارت دیگر برای حفظ محدودیت 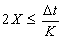، راه حل افزایش نسبت Δt / K است.

همانطور که گفته شد، Δt قبلاً انتخاب شده است، بنابراین تنها امکان کاهش مقدار K است. این به این معنی است که سطح دستیابی بیش از حد طولانی است و باید در تعدادی از N زیر دستیابی ها (N-1) تقسیم شود. زمان انتشار سیل K_j در امتداد j با نسبت بین طول l_j و طول L کل رسیدن متناسب در نظر گرفته می شود (Serban, 1984):

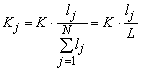
توجه داشته باشید که فاکتور وزن X ثابت است.

اگر تمام زیرمجموعه های N طول l_j یکسانی داشته باشند، پس:

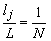
و رابطه می شود:

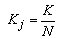
محدودیت هایی که از منفی نبودن پارامترها بدست می آیند در این مورد وجود دارد:

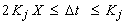
یا، با در نظر گرفتن رابطه بالا نتیجه حاصل می شود:

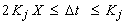
تعداد N از زیرمحدوده هایی که دسترسی در آن تقسیم می شود از رابطه حاضر بدست می آید:

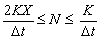
پس از ارزیابی تعداد زیرشاخه ها، می توان مقادیر تقریبی پارامتر K_j را با استفاده از رابطه بالا محاسبه کرد. با در نظر گرفتن ثابت X در طول رسیدن، پارامترهای a_j, b_j وc_j با جایگزینی در روابط حاضر، پارامتر K توسط پارامتر K_j بدست می آیند. محاسبه انتشار سیلاب به طور پی در پی در هر زیر دستی انجام می شود، تخلیه خروجی از یک زیرگذر تخلیه ورودی در زیر دستی بعدی پایین دست است (شکل 9.5).

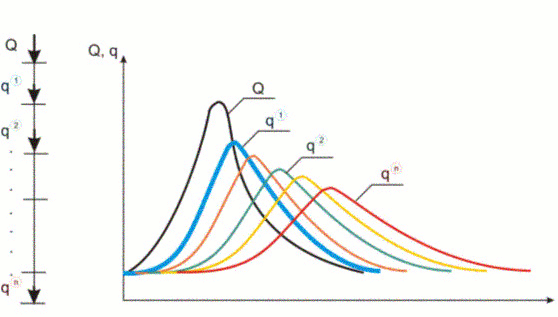
شکل 9.5 مسیریابی متوالی موج سیل.

امکان دیگر برای حل بی ثباتی در صورت رسیدن به مسافت طولانی، ایجاد روابط ریاضی حاصل از یک برنامه پی در پی از مدل ماسکینگام برای هر زیر دستی است (Drobot and Moldoveanu, 1995).

بگذارید تعداد زیر دست ها را با n مشخص کنیم. تخلیه پایین دست برای 2 زیرمجموعه عبارت زیر را دارد:

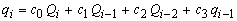
در صورت رسیدن به 3 زیرمجموعه، میزان مشابه قبلی بخش:

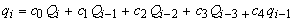
با تعمیم می توان تخلیه پایین دست را در انتهای زیرمجموعه n^th عنوان نوشت:

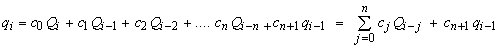
محدودیت غیر منفی باید با هر ضریب تأیید شود:

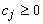
اگر نتیجه ضریب اول منفی باشد، این بدان معنی است که به دلیل فاصله زیاد بین انتهای رسیدن، تخلیه های بالادست مربوطه تأثیری بر تخلیه های فعلی در انتهای پایین دست ندارند. در نتیجه، آنها ناپدید خواهند شد و رابطه نهایی انتشار این است: (Drobot and Moldoveanu, 1995):

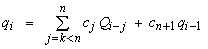
که در آن k شاخص تاخیر است.

برای مثال، اجازه دهید هیدروگراف های ثبت شده موج سیل (شکل 10.5) را در آوریل 1982 در دو ایستگاه هیدرومتری متوالی در رودخانه پروت (رومانی) بررسی کنیم. زمان انتشار موج سیل حدود 22 ساعت بود. مرحله زمانی 4 ساعته انتخاب شد و دسترسی به 5 زیر دستی تقسیم شد. معادله انتشار زیر پس از کالیبراسیون بدست آمد:

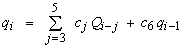
ضرایب عبارتند از: c₃=0.208; c₄=0.105; c₅=0.204; c₆=0.415. توجه داشته باشید که مجموع آنها: c₃+c₄+c₅+c₆=0.932<1. این نتیجه با این واقعیت که هیدروگراف پایین دستی دارای حجم کمتری نسبت به هیدروگراف بالادست است، کاملاً توجیه می شود.

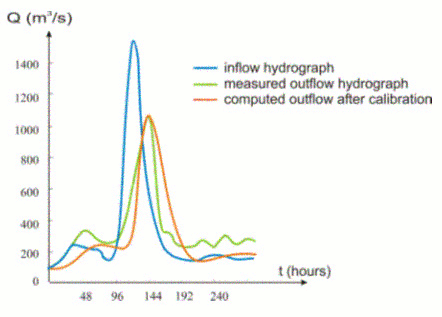
شکل 10.5 آوریل 1982 موج سیل در رودخانه Prut: هیدروگراف های پایین دستی ثبت شده و مدل سازی شده است.

د) شناسایی پارامترهای مدل Muskingum

- روش گرافیکی.

مطابق با رابطه اساسی، ذخیره ذخیره آب در رودخانه در لحظه من می تواند به عنوان محصول وزن سنگین تخلیه وزن و زمان K انتشار سیل بیان شود:

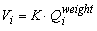
جایی که:

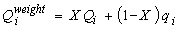
همانطور که در رابطه بالا مشاهده می شود، ذخیره و تخلیه به طور خطی وابسته هستند. از آنجا که تخلیه اولیه Q₀ صفر نیست، خط همبستگی از مبدا مختصات عبور نمی کند بلکه از نقاط مختصات (0, Q₀) عبور می کند. ایده روش گرافیکی رسم نقاط مختصات (Q_i^weight, V_i) و تقریبی آن توسط یک خط است که شیب آن فقط پارامتر K است.

مقادیر دشارژهای وزنی با توجه به رابطه محاسبه می شوند. در هر لحظه، تخلیه های Q_i و q_i مشخص هستند، اما X ناشناخته است. مقادیر دلخواه در بازه [0؛ 0.5] به X داده می شود و این مقدار که بهترین تقریب مجموعه {(Q_i^weight, V_i)} را با یک خط مستقیم ارائه می دهد، انتخاب می شود (شکل 11.5). سرانجام، مقدار پارامتر K به عنوان شیب این خط بدست می آید.

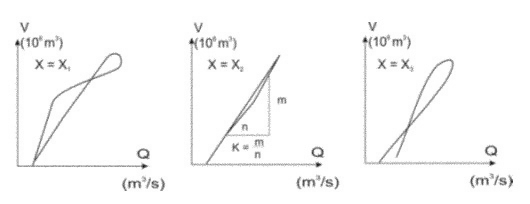
شکل 11.5 حلقه های ذخیره سازی و شناسایی پارامترهای K و X.

حجم های V_i با استفاده از رابطه محاسبه می شوند:

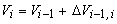
افزایش ذخیره سازی عبارت زیر را دارد:

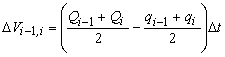
توضیح گرافیکی این روش در شکل 12.5 قابل مشاهده است.

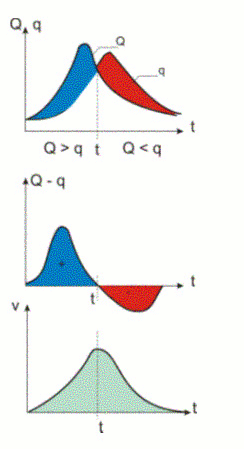
شکل 12.5 ذخیره آب در دسترس.

در مرحله اول فرآیند انتشار، زیرا Q (t)> q (t)، آب به طور موقت در بستر عمده رودخانه ذخیره می شود و منجر به افزایش مداوم حجم V می شود. این احتباس آب موقت میرایی موج را در هنگام طغیان بستر بزرگ توضیح می دهد. حداکثر V زمانی حاصل می شود که Q (t) = q (t) ؛ بعد از این لحظه، Q (t) <q (t)، اختلاف تخلیه منفی است و حجم ذخیره شده کاهش می یابد.

به فرآیند یافتن مقادیر پارامترهای مدل، کالیبراسیون گفته می شود. پارامترهای K و X به دست آمده توسط کالیبراسیون باید تأیید شوند. این بدان معنی است که وقتی از آنها برای سایر امواج سیل استفاده می شود، هیدروگراف پایین دستی محاسبه شده با هیدروگراف های ثبت شده مطابقت خوبی دارد. اگر عملکرد خطای پایین دستی قابل قبول باشد، می توان از پارامترها برای پیش بینی انتشار سیل استفاده کرد. اگر خطا خیلی بزرگ است، باید فرآیند کالیبراسیون، با استفاده از رویداد ثبت شده دیگر یا بهتر از بیش از یک سیلاب، تکرار شود. اگر بیش از یک سیلاب برای کالیبراسیون در دسترس باشد، بخشی از این وقایع برای کالیبراسیون و قسمت دیگر برای اعتبار سنجی استفاده می شود.

- چند همبستگی خطی

رابطه ماسکینگوم را می توان به عنوان یک همبستگی خطی چندگانه درک کرد (Drobot, 1983; Drobot, 1987). در نتیجه کالیبراسیون، پارامترهای a، b و c بدست می آیند.

رابطه انتشار سیل به صورت زیر نوشته خواهد شد:

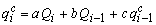
جایی که:

•  q_i^c جریانهای محاسبه شده در انتهای پایین دست بخش رودخانه را نشان می دهد
•  Q_i جریانهای اندازه گیری شده بالادستی هستند

جریان های پایین دستی اندازه گیری شده با q_i^m نشان داده می شوند.

تابع هدف مورد استفاده با روش حداقل مربعات:

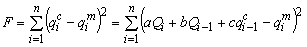
وقتی تابع F به حداقل خود می رسد، هر اصطلاح از مجموع تا حد ممکن کاهش می یابد، بنابراین می توان این _i^c ≈ q_i^m را تصور کرد (Drobot, 1983). با جایگزینی شاخص i با i-1، می توانیم q_i-1^c ≈ q_i-1^m بنویسیم و تابع هدف تبدیل می شود:

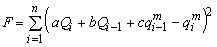
به این ترتیب ضرایب پارامترهای a، b و c شناخته می شوند. با محو مشتقات جزئی ∂F/∂a, ∂F/∂b, ∂F/∂c سیستم زیر از معادلات خطی بدست می آید:

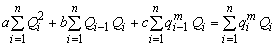
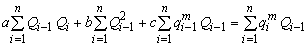
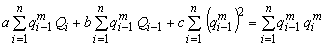
راه حل های a، b و c پارامترهای مورد استفاده برای انتشار سیل هستند. اگر پارامتر a منفی باشد، این بدان معنی است که طول دستیابی بیش از حد بزرگ است و باید آن را به زیرمجموعه ها تقسیم کرد.

2.1.5 شکل انتگرال مدل Muskingum

برای بدست آوردن معادله دیفرانسیل می توان معادله تداوم و رابطه انتشار مدل ماسکینگام را ترکیب کرد:

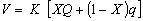
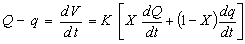
Chocat حل این معادله را با استفاده از شرایط اولیه مناسب در سال 1978 ارائه داد. اگر شرایط اولیه عبارتند از: q_t=0 = Q_t=0 = 0 سپس (Musy, 1998) در رابطه:

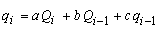
ضرایب a، b و c عبارات زیر را دارند:

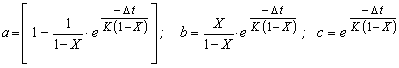
ضرایب a، b و c محدودیت های موجود را تأیید می کند زیرا در شکل مجزا مدل Muskingum مجموع آنها برابر با واحد است و غیر منفی هستند. از شرایط:

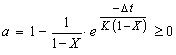
نتیجه می شود که:

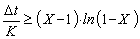
از نمایش گرافیکی (شکل 13.5) حوزه پایداری در صورت گسسته و شکل انتگرال مدل ماسکینگام، می توان دریافت که فرم انتگرال پایدارتر است (Musy, 1998).

شکل 13.5 ثبات عددی مدل Muskingum.

3.1.5 مدل Muskingum با پارامترهای متغیر

در مدل کلاسیک Muskingum، پارامترهای K و X در مقابل تخلیه ثابت نیستند. با این حال، برخی از تحولات بیشتر، تنوع پارامترها را در نظر می گیرند.

در مرحله اول، پارامتر X نسبت به نوسان تخلیه حساسیت کمتری در نظر گرفته و ثابت تلقی می شود (Ven Te Chow, 1964). برعکس، زیرا سرعت آب با تخلیه لحظه ای متغیر است، به این معنی است که زمان انتشار سیلاب در دسترس ثابت نیست.

تغییر K با تقسیم طول رسیدن به میانگین سرعت در رسیدن بدست می آید که تابعی از تخلیه ورودی بالادست است (Serban, 1984). هنگامی که دبی افزایش می یابد، زمان انتشار به حداقل مقدار Q_f کاهش می یابد، تخلیه مربوط به طغیان عمده رودخانه است. برای تخلیه بیشتر، به دلیل انتشار در منطقه ای با ضریب زبری بیشتر، سرعت کاهش می یابد و منجر به افزایش زمان انتشار می شود (شکل 14.5).

شکل 14.5 تغییر معمول پارامتر.

در رومانی نیز برخی مدل ها با درنظر گرفتن تنوع هر دو پارامتر K و X ساخته شده اند، که در واقع به معنای تغییرپذیری ضرایب a، b و c است. رابطه 5.14 به شکل زیر نوشته شده است (Drobot, 1987):

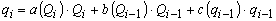
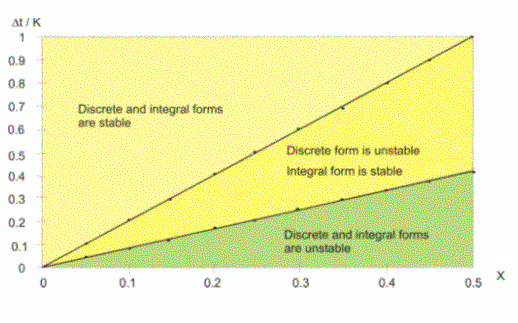
برای ضرایب a(Q_i), b(Q_i-1), c(q_i-1) برخی از توابع مختلف (توابع نمایی و قدرت، عبارات چند جمله ای و غیره) آزمایش شدند. بهترین نتایج برای عبارات زیر a، b و c بدست آمده است:

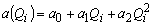
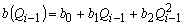
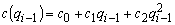
در این مدل از شرایط ذخیره سازی صرف نظر شد. در نتیجه، مجموع ضرایب لزوماً برابر با وحدت نیست. شرایط حفاظت احترام گذاشته می شود یا بستگی به فرایندهایی که در بستر عمده رودخانه رخ می دهد ندارد. تلفات ذخیره (آب ذخیره شده در فرو رفتگی های طبیعی، نفوذی یا تبخیری) می تواند نمایانگر چند درصد باشد، که منجر به اختلاف متناظر مجموع سه ضریب می شود.

مدل Muskingum با پارامترهای متغیر بدین ترتیب تبدیل می شود:

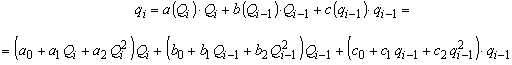
تابع هدف مدل تابع خطا است:

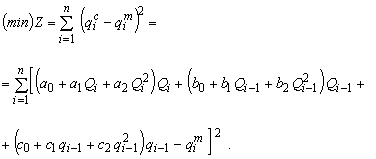
از آنجا که مورب اصلی غالب نیست، حل کلاسیک با از بین بردن اولین مشتقات با مشکلات عددی روبرو می شود. در نتیجه توصیه می شود از الگوریتم های برنامه ریزی غیر خطی استفاده کنید (به فصل 12 مراجعه کنید). به منظور وادار کردن مدل به بهترین شکل موج ثبت شده سیلاب پایین دست، یعنی در واقع شناسایی دقیق تر پارامترها، بعضی از ضرایب وزنی در بیان تابع هدف معرفی شدند. این ضرایب برابر با نسبت بین تخلیه های لحظه ای و جمع کل مقادیر گسسته شده تخلیه های پایین دست است.

تابع هدف تبدیل می شود به:

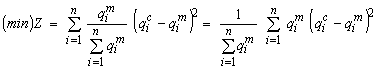
از آنجا که 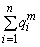 یک ثابت است که منوط به بهینه سازی نیست، عملکرد هدف این است:

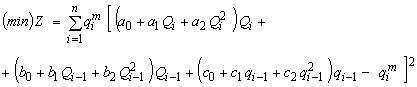
پارامترهای بدست آمده با استفاده از این تابع هدف بهترین تناسب را در حداکثر تخلیه هایی دارند که وزن بیشتری نسبت به تخلیه های کوچکتر دارند.

به عنوان مثال، در شکل 15.5 تغییر پارامترهای a، b و c برای این مدل ارائه شده است.

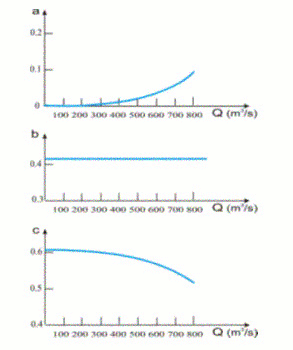
شکل 15.5 تغییر پارامترها.

لازم نیست که همه پارامترها به صورت چند جمله ای درجه دو بیان شوند. به عنوان مثال، برای پارامتر a، که تأثیر کمی دارد، ممکن است یک عبارت خطی یا حتی یک ثابت استفاده شود. ملاک انتخاب نوع بیان ریاضی برای پارامترها تولید مثل تخلیه پایین دست با دقت قابل قبول است.

4.1.5 مدل Muskingum با استفاده از یک عملکرد هسته غیر خطی

دسترسی رودخانه را می توان به عنوان یک سیستم جعبه سیاه مشاهده کرد که ورودی Q را به ورودی q از طریق یک عملکرد هسته غیر خطی u تبدیل می کند، متغیر با پالس Q (Amoro-cho, 1961; Dooge, 1973; Serban et Corbus, 1987 - referenced by Serban et al., 1989):

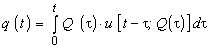
پس از گسسته سازی این رابطه به شرح زیر است:

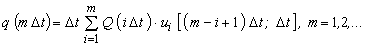
جایی که:

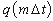•   مختصات هیدروگراف خروجی در لحظه mΔt
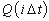•   جریان متوسط ​​در فاصله، شروع با لحظه iΔt ؛
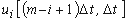•   مختصات در لحظه (m-i + 1) Δt از عملکرد هسته

به یاد بیاورید که عملکرد هسته خروجی سیستم را در یک پالس واحد نشان می دهد، که به طور یکنواخت در فاصله زمانی Δt توزیع می شود.

5.1.5 روش Muskingum-Cunge

Cunge (1969) یک عبارت تحلیلی برای پارامتر X بدست آورد، که شامل دوگانه بودن ارتفاع و دبی آب نیست:

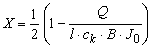
جایی که:

•  Q تخلیه
•  l طول دسترسی
•  B عرض سطح آب
•  J₀ شیب پایین
•  c_k ارتفاع موج حرکتی، دارای این عبارت:

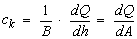
 مقدار 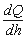 از منحنی رتبه بندی بدست می آید.

Cunge نشان داد که برای ثبات عددی، پارامتر X باید همان محدودیت هایی را که در مدل کلاسیک Muskingum وجود دارد را برآورده کند: 0 ≤ X ≤ 0.5. از رابطه حاضر می توان دریافت که l و X مستقل نیستند: مقدار X با افزایش طول l رسیدن و بالعکس افزایش می یابد (Popa, 1997). حداقل طول رسیدن از شرایط ناپدید شدن X حاصل می شود:

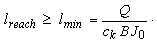
پارامتر K با رابطه بدست می آید:

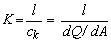
سمت راست معادله نشان دهنده زمان انتشار تخلیه معین در امتداد طول است. در روش Muskingum-Cunge هر دو X و K از نظر زمان و در امتداد رودخانه متغیر هستند. مقادیر آنها با استفاده از روابط موجود محاسبه می شود. برای انتشار موج سیل، دانستن X و K ضرایب C₁, C₂ و C₃ را می توان با روابط بالا بدست آورد. سرانجام انتشار با رابطه 5.14 انجام می شود.

مدیر سایت: بهزاد سرهادی

شماره تلفن: 09190622992

شناسه تلگرام مدیر سایت: SubBasin@

نشانی ایمیل: behzadsarhadi@gmail.com

(سوالات تخصصی را در گروه تلگرام ارسال کنید)

_______________________________________________________

پروژه تخصصی در لینکدین

×

 براي پيوستن به بزرگترين گروه تلگرام علوم و مهندسي آب با امکان تبادل نظر بين اعضاء کليک کنيد

کتاب کاربرد مدل QUAL2KW

کتاب کاربرد GIS در منابع آب

کتاب محاسبه سيل طرح