مجموعه آموزش هیدرولوژی - روشهای جستجوی عددی واسنجی مدل
2.11 روشهای جستجوی عددی
روشهای تحلیلی کلاسیک به ندرت در مسائلی استفاده می شود که شامل شناسایی پارامترها باشد زیرا بسیاری از اوقات توابع هدف عبارات پیچیده ای دارند یا حتی نمی توان آنها را به صورت تحلیلی تعریف کرد.
در این موارد از روش های عددی برای ارزیابی بهترین پارامترها استفاده می شود. فرآیند محاسبات یک فرایند تکراری است. این از یک راه حل اولیه شروع می شود، که باید در مورد یک مشکل محدود یک نقطه عملی باشد. با تکرارهای پی در پی، توالی تقریبی تولید می کند که به یک نقطه مطلوب همگرا می شود (که بهینه کلی لازم نیست). جستجو هنگامی که برخی از معیارهای همگرایی مطلوب است متوقف می شود و آخرین نقطه واقع شده پیکربندی بهینه پارامترها را نشان می دهد.
روش های جستجوی عددی دو نوع هستند:
- روشهای استفاده از مشتقات تابع هدف (روشهای گرادیان نامیده می شود) ؛
- روشهایی که از مشتقات تابع هدف استفاده نمی کنند.
1.2.11. روشهای گرادیان
ایده زیربنای این روشها در شکل 5.11 شرح داده شده است.
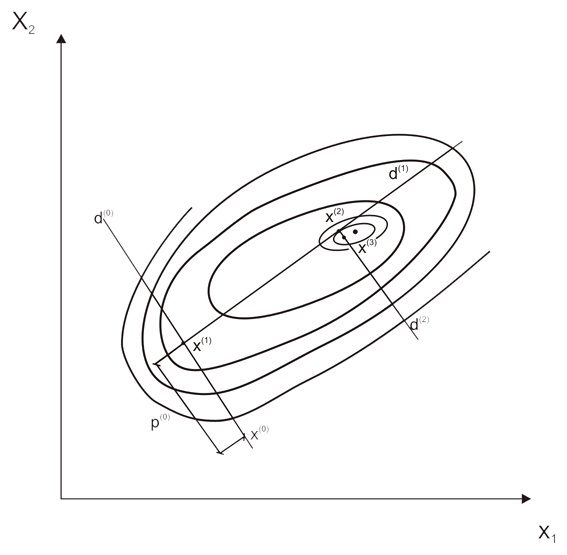
شکل 11.5 اساس روش های گرادیان.
ما از نقطه اولیه x(0) در امتداد جهت d(0) شروع می کنیم. با فرض اینکه ما در حال جستجو برای حداقل هستیم، نتیجه می شود که d(0) باید با جهت شیب دار نزول مطابقت داشته باشد. ما در امتداد این جهت حرکت می کنیم تا زمانی که فرود پایین بیاید. این بدان معنی است که حداقل جهت d(0) بدست آمده است. یک بخش عمودی از طریق سطح f(x1,x2) در امتداد جهت d(0) در شکل 11.6 رسم شده است. در این شکل d(0) مخفف abscissa است، در حالی که مقادیر تابع g(x) نشان دهنده تقاطع سطح f(x1,x2) و صفحه عمودی حاوی d(0) بر روی محور مختصات نشان داده شده است.
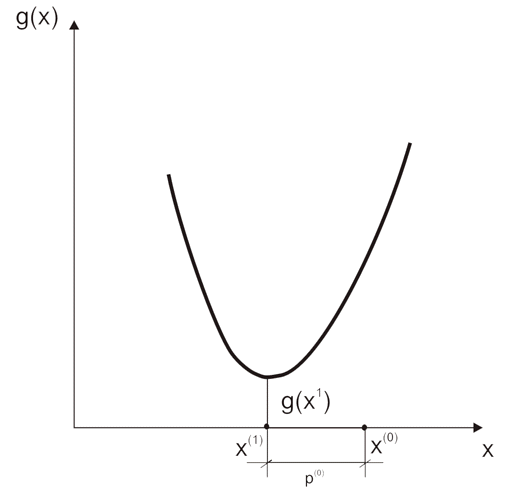
شکل 6.11 مقطع عمودی از طریق جهت.
فاصله p0 بین نقاط x(0) و x(1) اندازه گام بهینه در امتداد جهت d(0) را نشان می دهد. بنابراین می توانیم معادله برداری زیر را بنویسیم:
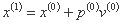
که ν(0) بردار واحد در جهت d(0) و p0 اندازه گام بهینه در جهت d(0) است.
با استدلال مشابه، از نقطه x(1) به نقطه x(2) با استفاده از رابطه حرکت می کنیم:
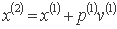
این را می توان به راحتی تعمیم داد به شرح زیر:
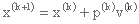
نقطه x(k) مشخص است. مقادیر p(k) و ν(k) باید مشخص شود.
ایجاد اندازه گام بهینه p(k) در تکرار k- مسئله جستجوی یک بعدی است، زیرا ما باید یک تابع را فقط در متغیر p به حداقل برسانیم. بنابراین ما می توانیم یا از حساب تحلیلی کلاسیک، متشکل از محو شدن مشتق، یا از روش های عددی استفاده کنیم.
در واقع، اگر جهت d(k) توسط بردار واحد ν(k) با پیش بینی ν1(k), ν2(k),... , νn(k) و مختصات نقطه x(k) تعریف شود x1(k), x2(k),... , xn(k) هستند، سپس
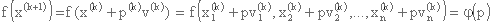
به این ترتیب که مقدار p(k)، اندازه گام بهینه در تکرار k-th، مقداری است که عملکرد φ(p) را به حداقل می رساند:
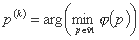
جهت d(k) به روشهای مختلف با هر روش شیب ایجاد می شود. به جلو ما دو مورد از آنها را ارائه خواهیم داد: روش تندترین نزول (بند 1.1.2.11) و روش فلچر-ریوز (بند 2.1.2.11).
هنگامی که هر دو رابطه زیر برآورده شوند، بهینه ترین حالت بدست آمده است:
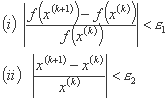
اگر f(x(k)) یا x(k) تمایل به صفر داشته باشد، باید شرایط توقف را برای جلوگیری از تقسیم بر صفر بیان کنیم:
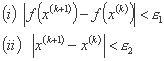
اگر ما فقط باید از شرط اول (i) استفاده کنیم، می توان قبل از دستیابی به حداقل روند در مواردی مانند شکل 11.7 روند را متوقف کرد.
به طور مشابه، در مناطق با شیب افزایش یافته، فاصله بین نقاط متوالی x(k) و x(k+1) بسیار کم است. فقط با استفاده از شرط دوم توقف، فرآیند بدون دستیابی به حداقل متوقف می شود.
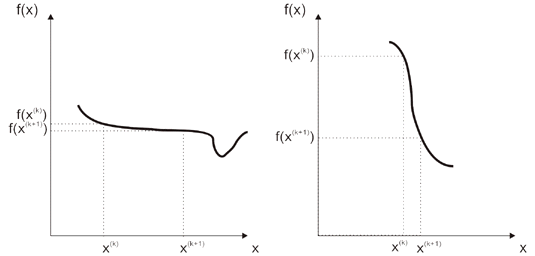
شکل 7.11 موارد بهینه کاذب الف) عملکرد تخت؛ ب) عملکرد شیب دار
1.1.2.11. روش پایین ترین شیب
شیب 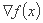 تابع f(x) در نقطه x = x(k)بردار اولین مشتقات جزئی است که در این نقطه ارزیابی می شود.
تابع f(x) در نقطه x = x(k)بردار اولین مشتقات جزئی است که در این نقطه ارزیابی می شود.
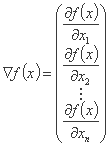 ;
; 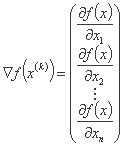
از نظر هندسی، شیب 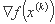 نشان دهنده بردار نرمال (متعامد) تا سطح سطح f(f) در x = x(k) است و در جهت تندترین صعود f(x). جهت دارد. بنابراین منفی بردار گرادیان جهت تندترین نزول را نشان می دهد و می توان از آن برای به حداقل رساندن عملکرد استفاده کرد.
نشان دهنده بردار نرمال (متعامد) تا سطح سطح f(f) در x = x(k) است و در جهت تندترین صعود f(x). جهت دارد. بنابراین منفی بردار گرادیان جهت تندترین نزول را نشان می دهد و می توان از آن برای به حداقل رساندن عملکرد استفاده کرد.
بنابراین جهت بهینه سازی d(k) به شکل زیر است:
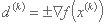
که در آن علامت "+" هنگامی که تابع باید به حداکثر برسد و علامت "-" هنگامی که به حداقل می رسد استفاده می شود.
بردار وحدت ν(k) با تقسیم بردار d(k) به طول آن بدست می آید که یک هنجار است 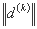 :
:
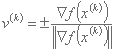
که در آن هنجار است:
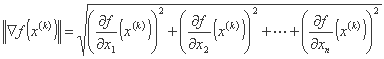
ما برای 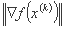 یک مقدار عددی بدست می آوریم که می تواند در اندازه گام بهینه باشد. بنابراین رابطه
یک مقدار عددی بدست می آوریم که می تواند در اندازه گام بهینه باشد. بنابراین رابطه
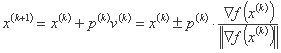
را می توان به شکل زیر نوشت:
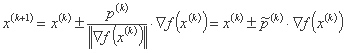
مزیت این رابطه این است که ارزیابی هنجار را غیرضروری می کند. همانطور که 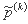 ، این به طور مستقیم با بهینه سازی تک بعدی نتیجه می شود.
، این به طور مستقیم با بهینه سازی تک بعدی نتیجه می شود.
2.1.2.11. روش فلچر-ریوز
این روشی از کلاس روشهای جهت مزدوج است که بدین ترتیب نامگذاری شده است زیرا جهتهای d(k) یک مجموعه بردار مستقل از بردار تشکیل می دهند.
علاوه بر این، ما از علامت گذاری زیر برای گرادیان استفاده خواهیم کرد:
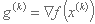
در صورت بروز مشکل به حداقل رساندن، روش در مراحل زیر خلاصه می شود:
الف) اگر نقطه اولیه x(0) را انتخاب کنیم، جهت اولیه d(0) منفی شیب در این نقطه است: d(0) = -g(0). توجه داشته باشید که عملکرد در این جهت کاهش می یابد:
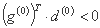
ب) نقطه جدید x(x+1) با توجه به رابطه تعیین می شود
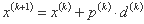
که در آن p(k) اندازه گام بهینه در جهت d(k) است.
ما همچنین شیب را در نقطه x(k+1): محاسبه می کنیم:
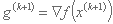
توجه داشته باشید که دو مرحله اول با روش تندترین فرود یکسان است.
ج) اما در ادامه راه، جهت d(k+1) را در (k + 1) انتخاب می کنیم - تکرار خاص این روش است:
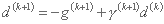
جهت جدید ترکیبی خطی از شیب در نقطه x(k+1) و جهت قبلی d(k) است که نقطه x(k+1) را ایجاد می کند.
ضریب γ(k+1) انتخاب می شود مانند جهت جدیدی که منجر به مزدوج (متعامد) به کل جهات قبلی است (این بدان معنی است که محصول داخلی آنها صفر است و از این رو یک مجموعه مستقل از بردارها را تشکیل می دهند).
از شرایط متعامد بودن نتیجه می شود که:
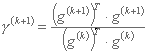
بنابراین جهت جدید d(k) توسط داده می شود
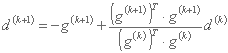
کاربرد روش فرض می کند که حداقل جهت d(k) دقیقاً در هر تکرار بدست آید. این بدان معنی است که اندازه گام p(k) مانند موارد زیر انتخاب شده است:
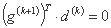
در صورت بروز یک مشکل حداکثر، رابطه محاسبات عبارت است از:
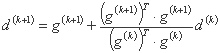
(که تغییر ساده نشانه ای از رابطه مورد استفاده در حداقل جستجو نیست).
3.1.2.11. شناسایی پارامترها با استفاده از روش های شیب
مدل MVICB
مدل Muskingum برای مسیریابی امواج سیل:
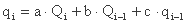 |
که در آن مجموع ضرایب برابر با واحد است.
تابع هدف برای شناسایی پارامترها مجموع مربعات انحراف بین جریانهای پایین دست محاسبه شده qic و مقادیر اندازه گیری شده qim است. به منظور نشان دادن منطقه جریان حداکثر به بهترین شکل ممکن، باید ضرایب وزنی را با wi معرفی کنیم:
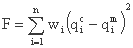
وزن wi متناسب با مقدار جریان فوری است. عبارات مختلف زیر را می توان برای wi پیشنهاد کرد:
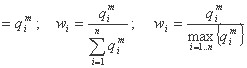
در مورد مدل با 3 پارامتر، مشتقات جزئی تابع هدف عبارات زیر را دارند:
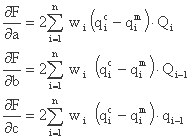
روش شیب دار نزول یک اشکال عمده دارد: میزان همگرایی آن می تواند بسیار کند باشد زیرا یک مسیر زیگزاگ به سمت محلول x * (حرکت با قدم های عمود) را دنبال می کند، بنابراین از نظر محاسباتی کارآمد نیست. در مورد روش فلچر-ریوز، حرکت با جهتهای مزدوج به حداقل نقطه، سرعت همگرایی بهبود یافته است.
ما در زیر نتایج مدل در مورد بخش Cosereni-Slobozia در رودخانه Lalomita ارائه می دهیم.
به دلیل طغیان گسترده در بستر رودخانه بزرگ در ژوئیه 1975، هیدروگراف امواج سیل دچار یک میرایی دیدنی شد (شکل 8.11) بین کوسرنی و اسلبوزیا.
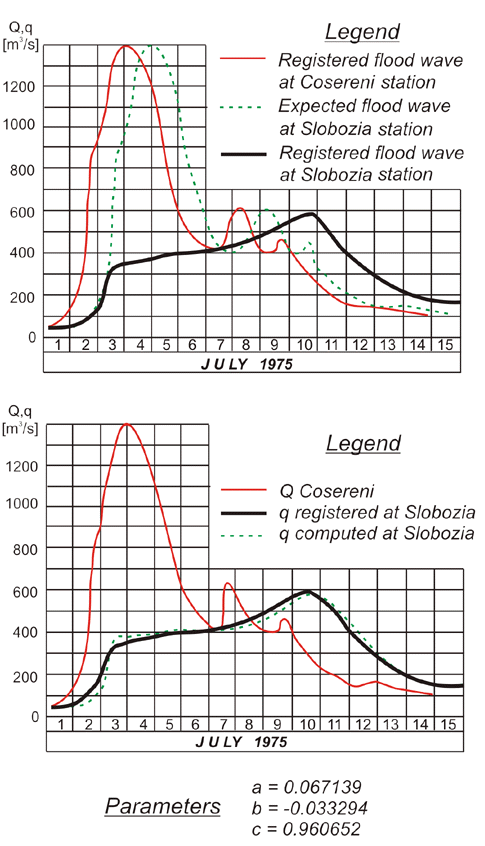
شکل 8.11 موج سیل در دسترس Cosereni-Slobozia در ژوئیه 1975.
همانطور که در شکل 8.11 مشاهده می شود، حجم ذخیره شده در بستر رودخانه طی دوره 1-8 ژوئیه بسیار بیشتر از حجم آزاد شده در دوره 8-15 ژوئیه است. این واقعیت که حجم موج سیلاب حفظ نشده است، استفاده از مدلهای کلاسیک Muskingum را با توجه به محدودیتهای آن غیرممکن می کند: مقادیر غیر منفی تمام پارامترها.
برخی تحقیقات (Serban & Corbus, 1987) منجر به تدوین مدلی شد که امکان شبیه سازی موج پایین دست را با دقت کافی فراهم می کند. با این حال این مدل دامنه تغییر فاکتور وزن X را از فاصله (0، 0.5) تا (-∞، 0.5) بزرگ می کند. این بدان معنی است که در نهایت ضرایب منفی پذیرفته می شوند.
با اجازه دادن به مدل برای یافتن پارامترهای بهینه خود، مقادیر زیر بدست آمد: a = 0.067؛ b = -0.033 ؛ c = 0.961. همانطور که پیش بینی شده بود، ضریب b منفی بود، زیرا بخشی از حجم سیلاب از بین می رود. ما یادآوری می کنیم که اگر ضریب a منفی باشد، فاصله بین انتهای بالادست و پایین دست بسیار زیاد است و ما باید بخش را در چندین زیر بخش تقسیم کنیم.
2.2.11. روشهای بهینه سازی بدون استفاده از مشتقات تابع هدف
در مشکلات بهینه سازی که در عمل بوجود می آیند، ما اغلب مجبوریم با یک تابع هدف غیرقابل تفاوت، یا علاوه بر این، تابعی روبرو شویم که نمی تواند به صورت تحلیلی تنظیم شود. حالت دوم، به عنوان مثال، با سیستم های دینامیکی اتفاق می افتد که در آن مدارها برای مقادیر گسسته آن زمان تعریف شده اند.
روشهایی که از مشتقات استفاده نمی کنند مقادیر تابع را در یک سری نقاط محاسبه می کنند و از این طریق جهت جستجوی جدید ایجاد می کنند. بدیهی است که زمان محاسبات مورد نیاز طولانی تر است، اما مزیت آن این است که این روش ها نیازی به عملکرد متغیر ندارند.
نتایج خوب با استفاده از هر یک از روش های زیر در عمل حاصل می شود:
- الگوریتم هوک و جیوز (همچنین "جستجوی الگو" نیز نامیده می شود) ؛
- الگوریتم روزنبروک ؛
- الگوریتم پاول ؛
- الگوریتم SIMPLEX Nelder و Mead ؛
- الگوریتم COMPLEX از Box.
ما در زیر فقط الگوریتم SIMPLEX Nelder and Mead را ارائه خواهیم کرد.
1.2.2.11. الگوریتم simplex
Simplex نمایانگر یک چند وجهی منظم با چند راس n + 1 به نام نقاط کاوشگر است که در آن مقادیر تابع هدف را محاسبه می کنیم. n تعداد ابعاد مسئله است 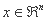 .
.
در حالت n = 2 hyper-polyhedron یک مثلث متساوی الاضلاع است، برای n = 3 simplex یک چهار ضلعی منظم است و غیره
در هر تکرار، مقادیر تابع هدف را در راس n + 1 راس بیش از چند وجهی محاسبه می کنیم و راس با بیشترین مقدار نامطلوب با یک نقطه جدید جایگزین می شود که ارزش عملکرد بیشتر است.
نکته جدید با پیش بینی نامطلوب ترین راس از طریق مرکز ثقل سایر راس های بیش از چند وجهی کاوشگر بدست می آید. وقتی موقعیت مرکز ثقل را محاسبه کنیم، نقطه نامطلوب مستثنی است.
طرح ریزی منجر به یکی از عملیات های زیر می شود: انعکاس، انبساط، انقباض I و انقباض II. مفهوم این فرقه ها در زیر توضیح داده خواهد شد، همانطور که الگوریتم را ارائه خواهیم داد. از آنجا که ما نامساعدترین راس را در هر تکرار طراحی و حذف می کنیم، نقاط کاوشگر 1+ به سمت منطقه ای که حد اکثر تابع هدف قرار دارد حرکت می کنند.
الگوریتم Nelder و Mead در مراحل زیر خلاصه می شود:
مرحله 1: ما یک نقطه شروع x(0) انتخاب می کنیم و یک ساده معمولی تولید می کنیم که توسط راس x1(0), x2(0), ..., xn+1(0) تشکیل شده است، جایی که:
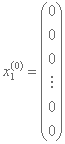
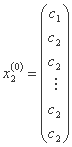
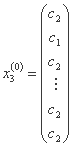 ...
...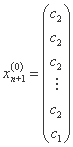
از نشانه های زیر استفاده شده است:
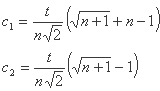
جایی که t مخفف فاصله راس های ساده ساده است.
مرحله 2: ما مقادیر عملکرد را در نقاط xi محاسبه می کنیم و راس های زیر را برجسته می کنیم:
xw "بدترین" راس مربوط به نامطلوب ترین مقدار تابع هدف است. به عنوان مثال، می توانیم بنویسیم:
در مورد حداقل مشکل
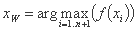
در حداکثر مشکل:
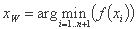
xUبعد از xw دومین راس نامطلوب است، بنابراین می توان نوشت:
در حداقل مشکل:
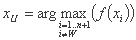
در حداکثر مشکل:
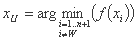
xB بهترین "راس" است که مربوط به مطلوب ترین مقدار تابع هدف است:
در حداقل مشکل:
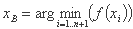
در حداکثر مشکل:
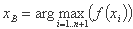
xC مرکز ثقل مربوط به تمام نقاط xi، i ≠ W است:
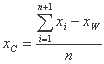
توجه داشته باشید که هنگام ایجاد مختصات مرکز، نقطه xw کنار گذاشته می شود.
مرحله 3: اکنون باید راس جدید ایجاد کنیم (شکل 9.11). ابتدا با بازتاب راس xR تولید می کنیم:
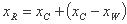
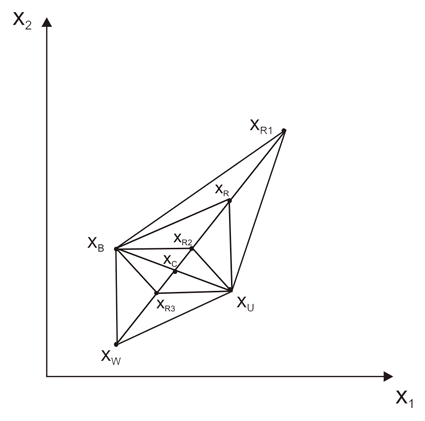
شکل 9.11 پیش بینی های بدترین نقطه در الگوریتم های Simplex.
الف) اگر مقدار عملکرد در xR بهتر از مقدار xB باشد ("بهترین" راس)، ما عملیات انبساط را انجام می دهیم، به این معنی که راس xR1 را تولید می کنیم:
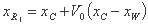
که معمولاً V0 = 2 است.
a ') اگر مقدار تابع xR1 بهتر از مقدار xB باشد، راس xw را با xR جایگزین می کنیم و مرحله 3 را ادامه می دهیم. ساده جدید (xB, xU, xR1) است.
a '') اگر نقطه xR1 "xB" از xB "بدتر" باشد، پس از آن Expandation شکست می خورد و x را جایگزین xw می کنیم و با مرحله 3 ادامه می دهیم. ساده جدید (xB, xU, xR) است.
ب) اگر مقدار عملکرد در xR بین xB و xU باشد، نه انبساط و نه انقباض توصیه نمی شود. ما xw را با xR جایگزین کرده و با مرحله 3 ادامه می دهیم. ساده جدید (xB, xU, xR) است.
ج) اگر مقدار تابع در xR نسبت به xU نامطلوب باشد، عملیات انقباض I یا II را اجرا می کنیم:
د) اگر مقدار عملکرد در xR بین xU و xW باشد، ما انقباض ساده (I) را انجام می دهیم، که جایگزین xW با xR2 است:
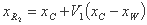
جایی که V1 = 0.5 است، و مرحله 3 را ادامه می دهیم. ساده جدید (xB, xU, xR2) است.
ه) اگر نقطه xR بدتر از xW باشد، انقباض II را اجرا می کنیم، که xR3 را جایگزین نقطه xW می کند:
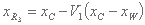
جایی که V1 = 0.5 است، و مرحله 3 را ادامه می دهیم.
فرایند تکراری با دستیابی به یکی از شرایط زیر متوقف می شود:
- لبه ساده از مقدار قابل قبول مجاز کمتر می شود.
- ریشه مربع حاصل از مجمع مربعات انحراف بین مقادیر تابع هدف در بهترین n راس سیمپلکس و مقدار تابع در مرکز ثقل کمتر از یک مقدار بحرانی است که پذیرفته شده است ،
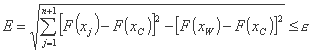
میانگین انحراف بین مقادیر تابع در راس های ساده و مقدار در بدترین نقطه کمتر از یک مقدار بحرانی است که پذیرفته شده است:
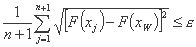
یا معادل آن
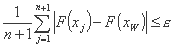
شکل 10.11 نحوه نزدیک شدن الگوریتم Nelder و Mead به نقطه مطلوب را در یک حالت دو بعدی نشان می دهد. از آنجا که n = 2، ساده یک مثلث متساوی الاضلاع است و 1، 2، 3 راس های آن را نشان می دهد. در طول تکرارها، مثلث شکل منظم خود را از دست می دهد، و به یک شکل مقیاسی تغییر می کند.
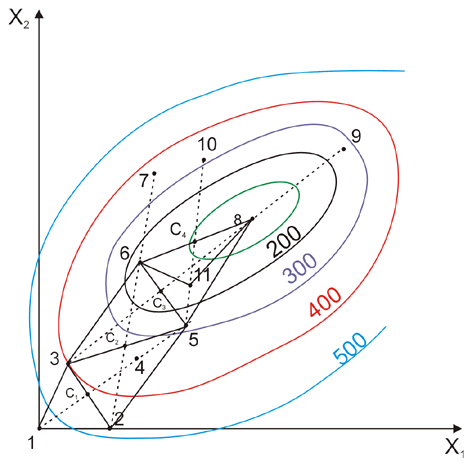
شکل 11.10 جستجوی بهینه با استفاده از الگوریتم Simplex.
نقاط اولیه 1، 2 و 3 است.
- تکرار اول: این تابع در نقطه 1 از نامطلوبترین مقدار برخوردار است. با محاسبه مختصات مرکز c1 (برای نقاط 2 و 3) متوجه می شویم که روی خط 2-3 قرار گرفته است، درست در وسط قطعه . بنابراین نقطه 1 از طریق c1 به نقطه 4 منعکس می شود و، چون تابع هدف در اینجا کمترین مقدار را دارد (حتی بهتر از نقطه 3، که مخفف xB است)، ما پسوند را به نقطه 5 انجام می دهیم. 1 در اولین تکرار حذف می شود و نقاط 2، 3 و 5 ساده جدید را تشکیل می دهند.
- تکرار دوم: با محاسبه مقادیر تابع در نقاط 2، 3 و 5 متوجه می شویم که نقطه 2 "بدترین" راس است. انعکاس 2 از طریق مرکز c2 ما را به نقطه 6 می رساند. تلاش برای گسترش به نقطه 7 ناموفق است زیرا مقدار عملکرد در 7 نسبت به نقطه 5 (که مخفف xB است) نامطلوب است. بنابراین نقاط 3، 5 و 6 ساده جدید را تشکیل می دهند.
- تکرار سوم: نقطه 3 ("بدترین" راس) از طریق c3 تا نقطه 8 پیش بینی می شود. از آنجا که مقدار عملکرد در این نقطه بهتر از راس 6 است، که مخفف xB است، ما گسترش راس 9 را انجام می دهیم. گسترش در نقطه 9 موفقیت آمیز نیست، و ساده جدید توسط نقاط تشکیل می شود 5، 6 و 8.
- تکرار چهارم: با رأس دادن راس 5 از طریق مرکز c4 به نقطه 10 می رسیم که مقدار عملکرد بیشتر از راس 5 است (که به معنای xw بود). بنابراین ما انقباض II را انجام می دهیم و به نقطه جدید، راس 11 می رسیم. ساده جدید توسط نقاط 6، 8 و 11 تشکیل می شود.
تکرارهای زیر انقباضات پی در پی را انجام می دهد که در همان زمان نزدیک شدن به نقطه مطلوب ضلع های ساده را کاهش می دهد.
2.2.2.11. شناسایی پارامترهای منحنی احتمال بیش از حد با استفاده از الگوریتم سیمپلکس
توالی کوتاه داده ها (n <30) منبع مهم خطاهایی را در حساب آماری تشکیل می دهد. این خطاها به دقت مربوط به ارزیابی ضریب تغییرات CV و ضریب عدم تقارن CS اشاره دارند.
ثابت شده است (یوویویچ، 1972) که ضریب تغییرات را می توان دقیق تر از ضریب عدم تقارن تعیین کرد. بنابراین در هیدرولوژی فقط CV از داده های اندازه گیری شده محاسبه می شود، در حالی که CS بر اساس تجربه عملی و توصیه ها بسته به CV انتخاب می شود. به طور معمول، CS = (2 - 4) CV
در صورتی که منحنی نظری با منحنی تجربی احتمالات بیش از حد مطابقت نداشته باشد، ضریب تغییرات CV را در فاصله تغییر می دهیم. ضریب CS با حفظ همان نسبت در مرحله اول تنظیم می شود.
به عنوان یک انتقاد از این فرایند، باید بگوییم که نسبت CS / CV مقادیر را از مرحله 1.0 به 4.0 می گیرد. این مش به اندازه کافی تیز نیست، از این رو حتی انعطاف پذیری منحنی های نظری پروبا نیز وجود دارد توانایی های بدست آمده توسط پارامترهای محاسبه شده گاهی کافی نیست. در حقیقت یافتن مقدار صحیح برای CV و انتخاب مناسب نسبت CS / CV مسئله شناسایی پارامترهای بهینه عملکرد تراکم احتمال حداکثر تخلیه های سالانه است.
پارامترهای تجزیه مجدد آماری را می توان با برنامه نویسی غیر خطی با استفاده از الگوریتم SIMPLEX Nelder and Mead بدست آورد (Drobot، 1989).
ما برای تقسیم نظری توزیع گاما با 3 پارامتر استفاده خواهیم کرد:
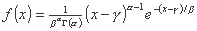
جایی که:
- α یک پارامتر شکل است
- β یک پارامتر مقیاس
- γ حد پایین مقادیر توزیع.
حال فرض کنید تجزیه تجربی زیر را داشته باشیم:
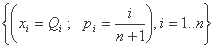
جایی که جریان های Qi به طور کمتری مرتب می شوند: Q1 > Q2 > ... > Qi > ... > Qn
از نظر ریاضی، مسئله در یافتن پارامترهای مناسب α، β، γ مانند مجموع مربعات انحراف بین احتمالات تجربی و حداقل موارد نظری است:
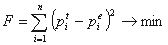
گودال احتمالات نظری بیش از جریان ثبت شده را می توان با روابط زیر ارزیابی کرد:
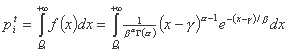
از این رو تابع هدف این عبارت را دارد:
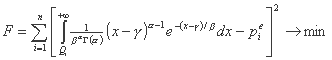
ما از روش گاوس با 16 امتیاز برای ادغام تابع چگالی احتمال استفاده کردیم. به منظور افزایش دقت حساب، ادغام گام به گام بین مقادیر اندازه گیری شده متوالی Qi و Qi+1 انجام شد. جایی که فاصله بین دو مقدار متوالی خیلی زیاد بود، آن را تقسیم کردیم.
مختصات حداقل نقطه، در این حالت، 3 پارامتر ناشناخته α، β، γ هستند که بهترین انطباق را بین منحنی تجربی و نظری دارند. این پارامترها ممکن است مستقیماً برای بدست آوردن جریانهایی با احتمال بیش از حد متفاوت یا برای محاسبه نسبت CS / CV استفاده شوند.
برای توزیع گاما با 3 پارامتر لحظه اول (میانگین)، به ترتیب لحظه های مرکز شده از مرتبه دوم و سوم عبارت زیر را دارند:
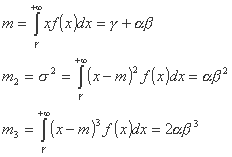
از این رو ضرایب تغییر و عدم تقارن عبارتند از:
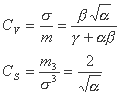
بسته به پارامترهای α، β، γ که توسط فرایند بهینه سازی تعیین می شوند، بلافاصله نسبت CS / CV را دنبال می کنیم.
این مدل برای محاسبه احتمالات نظری بیش از حد در صورت توالی کوتاه (25 = n) حداکثر جریان سالانه در ایستگاه فروموسو در رودخانه بیستریتا ثبت شده است (شکل 11.11).
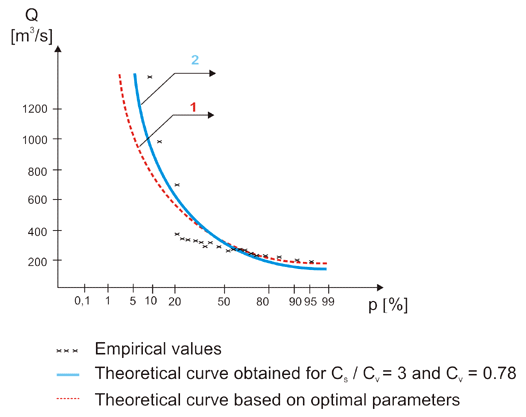
شکل 11.11 مقایسه بین منحنی های مختلف احتمالات بیش از حد.
پارامترهای حاصل از فرآیند به حداقل رساندن عبارتند از:
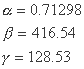
و آنها به مقادیر زیر برای میانگین، ضرایب تغییر و عدم تقارن منجر شدند:
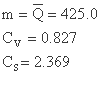
بنابراین CS / CV = 2.86. در شکل 12.11 مقادیر تجربی و منحنی نظری ترسیم شده برای پارامترهای بدست آمده توسط بهینه سازی (منحنی 1) نشان داده شده است.
برای مقایسه، ما همچنین منحنی نظری احتمال بیش از حد را با استفاده از روش لحظه ها حل و فصل کردیم. مقادیر بدست آمده برای میانگین و ضریب تغییر عبارت بودند از:
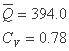
با تنظیم CS / CV = 3 (مقدار پیشنهادی با نسبت بدست آمده از طریق فرآیند بهینه سازی)، CS = 2.34 بدست خواهیم آورد.
در شکل 11.11 همچنین برای مقایسه منحنی نظری (منحنی 2) برای پارامترها و CV حاصل از روش گشتاورها (با نسبت CS / CV = 3) ارائه شده است. حتی اگر نسبت CS / CV را نیز به درستی انتخاب کنیم (چیزی که همیشه در عمل نمی توان انجام داد)، تقریب منحنی تجربی ضعیف تر از آن است که با پارامترهای بدست آمده از بهینه سازی به دست آمده است.
3.2.11. چندین راه حل برای مشکلات محدود
1.3.2.11. روش تابع جریمه
همانطور که قبلاً گفتیم، یک مسئله بهینه سازی عمومی را می توان به شکل زیر نشان داد:
بهینه سازی f (x)، با توجه به موارد زیر:
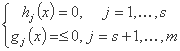
این مسئله محدود را می توان به یک مسئله غیرقانونی معادل از نوع زیر تبدیل کرد:
بهینه سازی
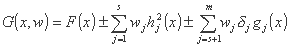
جایی که:
- G(x,w) را تابع جریمه می نامند
- wj > 0 ضرایب حریمه را نشان می دهد
اگر محدودیت های برابری hj(x) = 0 برآورده شود، اصطلاحات مربوطه هیچ تاثیری بر عملکرد G(x,w) ندارند. اگر hj(x) ≠ 0، آنگاه ما نیز داریم 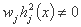 و مقدار G(x,w) تحت تأثیر قرار می گیرد.
و مقدار G(x,w) تحت تأثیر قرار می گیرد.
ما می توانیم یا hj(x) < 0 یا hj(x) > 0 داشته باشیم. برای از بین بردن تأثیر علامت محدودیت های نقض شده، در بیان G(x,w)، از مربعات توابع hj(x) استفاده می کنیم. اگر مجبور شویم F(x) و در نتیجه G(x,w) را به حداقل برسانیم، علامت استفاده شده در مقابل مبالغ "+" است. مقدار G(x,w) به این ترتیب افزایش می یابد و الگوریتم محدود به جستجوی راه حل های دیگر است تا زمانی که سهم اصطلاحاتhj(x) از بین برود. اگر یک مشکل حداکثر سازی داشته باشیم، علامت مورد استفاده "-" است به همان دلیل قبلی: برای کاهش مقدار G(x,w) در صورت عدم رضایت محدودیت ها.
عوامل δj نشانگر عملگرهای منطقی است که مقادیر زیر را می گیرند:
δj = 0 if gj(x) ≤ 0 (محدودیت ها رعایت می شوند)
δj = 1 if c(x) > 0 (محدودیت ها نقض می شوند).
برای جمع دوم ضرایب wj نیز همان نقش را دارند که مجازات نقض محدودیت ها را مجازات می کنند. تفسیری که در بالا در مورد علامت "+" یا "-" ارائه دادیم نیز در این حالت وجود دارد: علامت "+" برای مشکلات به حداقل رساندن و "-" برای موارد حداکثر استفاده می شود.
بهینه تابع G(x,w) که مبالغ ناشی از محدودیت برای آن از بین می رود مربوط به بهترین مقدار F (x) است. به عبارت دیگر، راه حل بهینه برای G(x,w) با نقطه مطلوب F(x) در منطقه عملی یکسان است (مجموعه تمام نقاطی که قیدهای hj(x) = 0 و gj(x) ≤ 0 را برآورده می کند)
ضرایب مجازات wj متفاوت است، به این معنی که آنها مقادیر بیشتری برای محدودیتهایی دارند که بیش از همه باید برآورده شوند، یا برای کسانی که هنوز در پایان فرآیند بهینه سازی رضایت ندارند. در حالت دوم، فرآیند با مقادیر تنظیم شده برای wj مجدداً شروع می شود.
تابع جریمه G(x,w) به همان صورت تابع لاگرانژ ساخته می شود و ضرایب wj به طور یکسان ضربی λj عمل می کنند. تفاوت در این واقعیت است که، در حالی که در روش لاگرانژ پارامترهای λj با بهینه سازی حاصل می شوند، در مورد تابع جریمه پارامترهای wjانتخاب می شوند تا مجبور شوند رضایت را برآورده کنند.
2.3.2.11. تکنیک به حداقل رساندن بی قید محدود (SUMT).
از آنجا که حداکثر f(x) = -min (-f(x))، ما فقط در زیر به حداقل مشکلات اشاره خواهیم کرد.
فرض کنید با مشکل محدود زیر روبرو هستیم:
F(x) را به حداقل برسانید، منوط به gi(x) ≥ 0, i = 1, ..., m.
ما راه حل *x آن را با حل بهینه مسئله نامحدود تقریبی می کنیم:
به حداقل رسانی
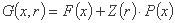
اگر راه حل فعلی x محدودیت ها را برآورده کند، تفاوت بین G(x,w) و F(x) بسیار کم است، اما، برای نقاط خارج از منطقه عملی، مقدار G(x,r) بیش از حد زیاد می شود ( در مسائل به حداقل رساندن) یا کم (در مسائل حداکثر) به دلیل عملکرد مجازات P(x).
در چنین مشکلات به حداقل رساندن، می توان از روش کارول استفاده کرد. این شامل دنباله ای از به حداقل رساندن عملکرد G(x,r) است
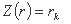
جایی که
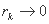
و
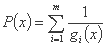
یا
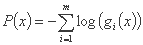 .
.
اکنون مشکلی را در نظر بگیرید که دارای محدودیت های برابری نیز هست:
F(x) را به حداقل برسانید، با توجه به موارد زیر:
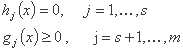
راه حل با جستجوی حداقل مسئله غیرقانونی معادل آن بدست می آید:
به حداقل برسانید
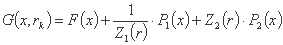
جایی که برای 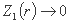 و
و 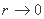 برای
برای 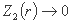 ، و
، و 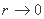 داریم P1(x) و P2(x) مجازات های کافی برای برابری، به ترتیب محدودیت های نابرابری هستند.
داریم P1(x) و P2(x) مجازات های کافی برای برابری، به ترتیب محدودیت های نابرابری هستند.
در فرمولاسیون های Fiacco و Mc Cormick عملکرد G(x,rk) عبارت زیر را دارد:
به حداقل برسانید
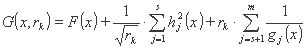
هر دو تکنیک (کارول، به ترتیب Fiacco و Mc Cormick) روشهای نقطه داخلی هستند زیرا راه حل اولیه در داخل منطقه عملی قرار دارد.
برخی از روشهای نقطه خارجی نیز وجود داشته است که هرگاه x یک نقطه عملی نیست، عملکرد G(x,r) را مجازات می کند. در صورت برآورده شدن محدودیت ها مجازات صفر است.
3.3.2.11. مطالعه موردی
در مرحله بعد، ما مسئله محدود مدل سازی ارزیابی بارش خالص همراه با یکپارچه سازی آن را ارائه خواهیم داد (Drobot & Iorgulescu، 1990).
ضریب رواناب را می توان با استفاده از رابطه زیر بیان کرد:
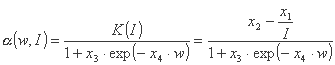
که در آن w اندازه گیری رطوبت خاک است و من شدت باران است.
بدیهی است که محدودیت های مربوط به حد پایین و بالا ضریب رواناب باید رعایت شود: 0 ≤ α(w,I) و α(w,I) ≤ 1
K(I) نشان دهنده حد بالای ضریب رواناب برای منحنی مربوط به شدت باران I است و در نتیجه باید شرایط را تأیید کند: 0 ≤ K(I) و K(I) ≤ 1
پس از ملاحظات مختلف جسمی، محدودیت های زیر را داریم:
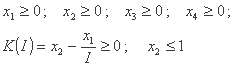
پارامترهای هیدروگراف واحد معمولاً توسط تابع گاما با دو پارامتر تعریف می شوند:
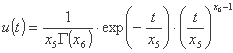
اگرچه از نظر تئوری تابع Γ(x6) برای مقادیر x6>0 تعریف شده است، اما در عمل، به دلایلی در مورد شکل هیدروگراف واحد، شرط زیر باید رعایت شود: x6 ≥ 1.
پارامتر یک عامل مقیاس را نشان می دهد، بنابراین باید همیشه کاملاً مثبت باشد: x5 > 0
برای نوشتن تابع جریمه G(x,w) محدودیت ها باید به صورت gj(x) ≤ 0 نوشته شوند
بنابراین باید محدودیت های xj ≥ xmin j و xj ≤ xmax j را به gj(x) = xmin j - xj ≤ 0 تبدیل کنیم، به ترتیب gj(x) = xj - xmax j ≤ 0
ملاحظات فوق ما را به شکل زیر محدودیت ها سوق می دهد:
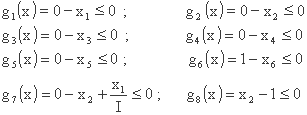
تابع هدف با تابع خطا (مجموع انحراف مربع بین مقادیر هیدروگراف اندازه گیری شده و محاسبه شده برای امواج سیلاب V) و اصطلاحات مجازات مربوط به محدودیت های فوق نشان داده می شود:
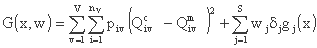
جایی که:
- Qivc جریان محاسبه شده در گام اول سیل (ν = 1,...,n)
- Qivm جریان را در همان مرحله از همان سیل اندازه گیری کرد
- gj(x) = 1، ...، 8 هشت محدودیت نسبت به پارامترهای مدل هستند
- wj j = 1، ...، 8 ضریب جریمه است
- δj j = 1، ...، 8 عملگرهای دودویی هستند که بسته به رضایت یا عدم محدودیت ها مقادیر 0 یا 1 را می گیرند
- piv وزن های متناسب با Qivm هستند
ما در زیر نتایج به دست آمده برای حوضه رودخانه بیستریتا در ایستگاه هیدرولوژیکی فروموسو را ارائه خواهیم داد. سطح حوضه هیدروگرافی 2813 کیلومتر مربع است. حد بالایی K(I) عبارات کمی اصلاح شده ای دارد:
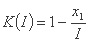 (case A)
(case A)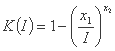 (case B)
(case B)
به منظور شناسایی پارامترها از 6 سیلاب در طی دوره 1972-1979 استفاده کردیم. محتوای اولیه رطوبت براساس همبستگی با جریان پایه محاسبه شد.
ما برای منحنی SSARR، به ترتیب برای هیدروگراف واحد، پارامترهای زیر را بدست آوردیم:
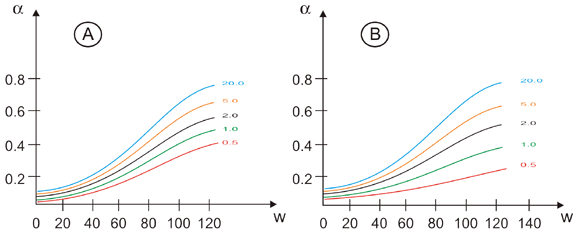
شکل 12.11 منحنی SSARR پس از کالیبراسیون پارامترها بدست آمده است.
شکل 12.11 منحنی های SSARR را نشان می دهد که با پارامترهای به دست آمده در هر دو حالت A و B نشان داده شده است، در حالی که در شکل 13.11 توافق بین هیدروگراف سیل اندازه گیری شده و مدل شده نشان داده شده است.
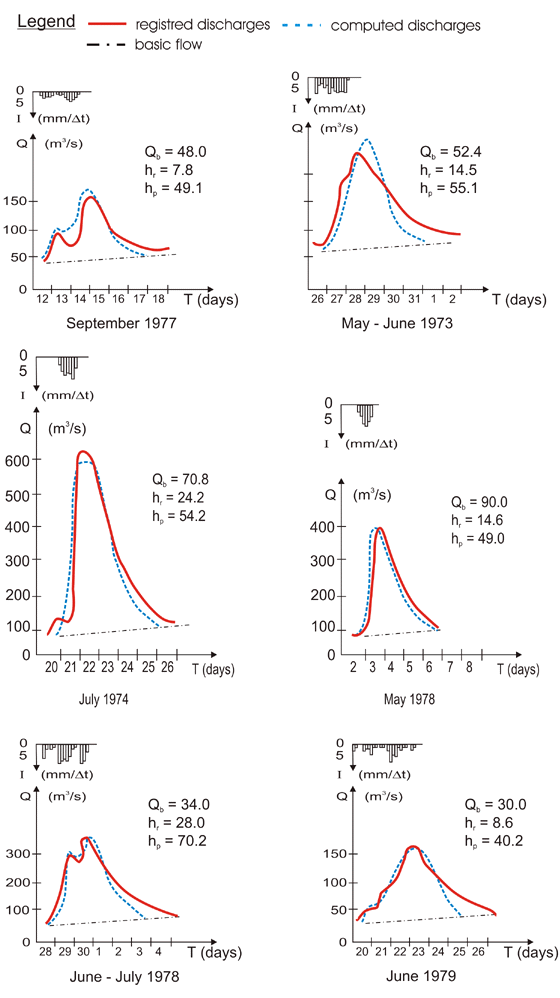
شکل 11.13 هیدروگراف های اندازه گیری شده و شبیه سازی شده در ایستگاه فروموسو.
لازم به ذکر است که، برای بدست آوردن نمایش دقیق منطقه زیاد سیل، از ضرایب وزنی متناسب با جریان فوری که باید شبیه سازی شود، استفاده کردیم.
از شکل 13.11 نیز می توان دریافت که سیلاب های محاسبه شده مدت زمان کمتری نسبت به اندازه گیری های اندازه گیری شده دارند، که این امر ضرورت معرفی مولفه پوست را به مدل تأکید می کند.
4.2.11. تبدیل مدلهای غیر خطی به مدلهای خطی
یک مدل برنامه ریزی غیر خطی را می توان با گسترش در مجموعه های تیلور، هم تابع هدف و هم توابع محدودیت، و فقط با استفاده از عبارات 0 و درجه 1 به یک مدل خطی تبدیل کرد. این به این معنی است که ما یک توابع خطی قطعه ای را با یک اندازه گام خاص از توابع غیر خطی اولیه انجام می دهیم.
در موارد خاص، اگر محدودیت ها خطی و تابع هدف بصورت قطعه ای خطی باشد، می توانیم به سادگی از برنامه ریزی خطی استفاده کنیم، بدون اینکه دیگر در سری تیلور گسترش یابد. بنابراین مدلهای برنامه ریزی خطی حاصل می شوند که دارای عملکرد هدف و همچنین محدودیتهای نوع خطی هستند.
پدیده هایی که در طبیعت ملاقات می شوند معمولاً غیرخطی هستند. خطی سازی یک فرضیه ساده است که مزایای مهمی از جمله:
- امکان نزدیک شدن به مشکلات ابعاد بزرگ، که با استفاده از تکنیک های غیرخطی منع کننده است.
- کارایی الگوریتم ها، هم در مورد زمان محاسبه و هم در شناسایی بهینه جهانی.
اما مدل بدست آمده با خطی سازی دقیقاً کمتر پدیده واقعی را بازتولید می کند، که معمولاً غیرخطی است، همانطور که قبلاً اشاره کردیم. بنابراین نقطه بهینه حاصل از استفاده از الگوریتم های ریاضی لزوماً نقطه بهینه مسئله واقعی نیست، اما تقریب مناسبی برای آن است. در نهایت بهینه مدل خطی می تواند نقطه شروع یک مدل غیرخطی باشد که واقعیت را با دقت بیشتری تولید می کند.
به عنوان یک قاعده، برنامه ریزی غیرخطی برای شناسایی پارامترها در صورت کم بودن تعداد آنها توصیه می شود. اما برای مشکلات با پیچیدگی بالا، رویکرد خطی اغلب تنها امکان عملی برای شناسایی پارامترها است. بنابراین، به عنوان مثال سیستم های هیدروژئولوژیکی منطقه ای.
1.2.4.11. رویکردهای خطی متوالی
بیایید مشکل بهینه سازی زیر را در نظر بگیریم:
به حداقل رساندن
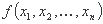
هدف
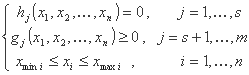
ما یک راه حل اولیه x(0) انتخاب می کنیم که محدودیت ها را برآورده کند. با گسترش توابع f, hj, gj در مورد نقطه x(0) مسئله اولیه به مدل خطی زیر تبدیل می شود:
به حداقل رساندن
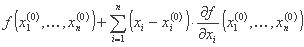
هدف
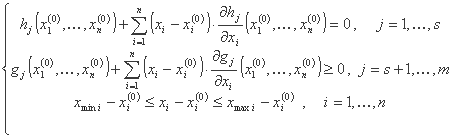
با استفاده از نشانه های زیر:
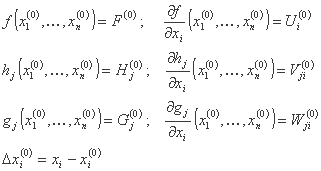
مدل خطی را می توان به صورت زیر نوشت:
به حداقل رساندن
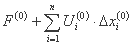
هدف
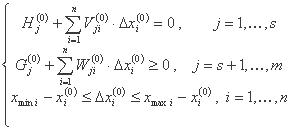
مقادیر F(0), Ui(0), Hj(0), Vji(0), Gj(0), Wji(0), xmin i - xi(0), xmax i - xi(0) مشخص است. مجهولات مسئله مراحل Δxi(0) است که باید با حداکثر مقدار مجاز Mi(0) محدود شود.
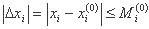
یا معادل آن:
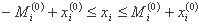
این مقدار حداکثر Mi(0) مانند اختلاف بین مقدار تابع خطی در انتهای مرحله مجاز ارزیابی می شود و مقدار تابع اصلی کمتر از مقدار مناسب ε است. بنابراین، Mi(0) محدودیت های زیر را برآورده می کند:
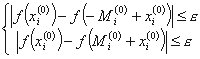
مدل بهینه سازی مقدار Mi(0) را تعیین نمی کند. تا زمانی که دو شرط فوق تأیید نشود، با آزمایش های پی در پی ایجاد می شود. پس از آن مدل بهینه سازی شروع به کار می کند. همچنین باید توجه داشته باشیم که مقدار Δxi می تواند مثبت یا منفی باشد. برای احترام به شرایط غیر منفی، ما باید تحول را معرفی کنیم:
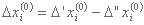
جایی که
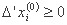
و
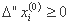
بنابراین مدل خطی به شکل زیر نوشته می شود:
به حداقل رساندن
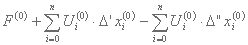
هدف
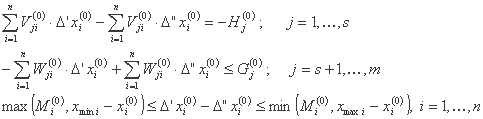
با حل این مسئله خطی باید مراحل ناشناخته Δxi(0) بدست آوریم. نقطه xi(0) با نقطه xi(1) جایگزین می شود، که با رابطه حاصل می شود:
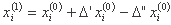
سپس مقادیر جدید توابع F, U, H, V, G, W را در نقطه xi (1) محاسبه خواهیم کرد: xi(1): F(1), Ui(1), Hj(1), Vji(1), Gj(1), Wji(1)
در ادامه مقدار حد مرحله Δxi(1) مشخص شده است و ما باید مسئله جدید را با ناشناخته های Δ' xi(1) و Δ'' xi(1) حل کنیم.
محاسبات تا لحظه ای که Δ' xi(k) ≈ Δ'' xi(k) ≈ 0 داشته باشیم ادامه می یابد، به این معنی که نقطه x(k) در نزدیکی بهینه جهانی است.
11.2.4.2. توابع عینی یک فرم خاص
همانطور که می دانیم، تابع خطا را می توان به صورت مجموع ماژول ها نیز نوشت. اگر رابطه بین مقادیر محاسبه شده و پارامترهای مدل خطی باشد و محدودیت ها نیز از نوع خطی باشند، بنابراین ممکن است برای شناسایی پارامترها از تکنیک های برنامه ریزی خطی استفاده کنیم.
تابع هدف به عنوان مجموع ماژول ها:
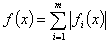
جایی که fj(x) تفاوت بین مقادیر محاسبه شده و اندازه گیری شده را نشان می دهد.
بردار x مجهولات نیز باید محدودیت های زیر را برآورده کند:
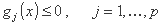
که در آن gj برخی از توابع خطی است.
ما متغیرهای کمکی yi تعریف شده را معرفی خواهیم کرد مانند:
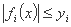
مشکل اولیه با مشکل برنامه نویسی زیر برابر است:
به حداقل رساندن
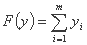
هدف
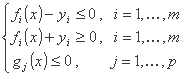
شناسایی پارامترهای مدل Muskingum
از روش قبلی می توان برای شناسایی پارامترهایی که در رابطه ماسکینگوم از انتشار امواج سیلاب بوجود می آیند استفاده کرد (Drobot, 1983; Drobot, 1984).
تابع هدف را می توان به صورت زیر نوشت:
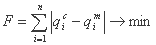
که در آن qic و qim مقادیر هیدروگرافی محاسبه شده و اندازه گیری شده پایین دست هستند.
ما برای هر اصطلاح تابع هدف حداکثر مقدار yi را معرفی خواهیم کرد:
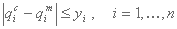
بنابراین می توان مشکل بهینه سازی را به صورت زیر نوشت:
به حداقل رساندن
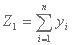
هدف
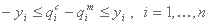
یا معادل آن
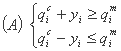 i = 1,K,n
i = 1,K,n
در مدل کلاسیک Muskingum، پارامترها باید داراس الزام زیر باشد:
a + b + c = 1
با در نظر گرفتن معادله انتشار، می توان آنرا چنین نوشت:
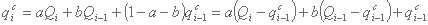
اصطلاح qi-1c ناشناخته است. می توان آن را با qi-1m جایگزین کرد، اگرچه بدیهی است که فقط درصورت yi-1 = 0 می توانند برابر باشند.
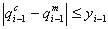
با جایگزینی qi-1c با qi-1m در معادله انتشار، رابطه اولیه تغییر می کند و علامت "=" باید با "≈" جایگزین شود:
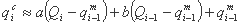
البته، تفاوت بین سمت چپ و سمت راست باید توسط یک مقدار xi محدود شود، که مانند yi، نیز در معرض بهینه سازی است. بنابراین می توانیم بنویسیم:
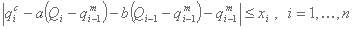
مقادیر کمتر برای xi، تناسب بین جریانهای محاسبه شده و اندازه گیری شده بهتر است. بنابراین می توان یک تابع دوم، Z2 نوشت:
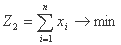
جایی که مجهولات xi محدودیت های زیر را برآورده می کند:
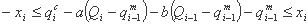 , i= 1,K,n,
, i= 1,K,n,
یا معادل آن
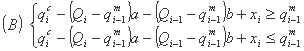 , i = 1,K,n,
, i = 1,K,n,
تابع هدف مدل افزودنی است که با جمع بندی توابع Z1 و Z2 تشکیل می شود:
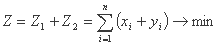
محدودیت های مسئله هر دو مجموعه (A) و (B) هستند.
همچنین ممکن است از توابع عینی با ضرایب وزن استفاده کنیم:
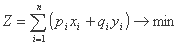
ضرایب pi و qi در ناحیه جریان حداکثر، جایی که دقت بهتری در محاسبات لازم است، بیشتر است و در ناحیه حداقل جریان، جایی که برخی اختلافات بین مقادیر محاسبه شده و اندازه گیری شده مجاز است.
در کنار مجموعه های (A) و (B) ارائه شده در بالا، مدل باید با محدودیت های دیگری تکمیل شود. ما از روابط شروع می کنیم:
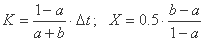
به دلیل معنای فیزیکی، ما K> 0 داریم، که به معنی 1-a> 0، یا a <1. همچنین، X> 0 است که شامل محدودیت است:
(C) b>a
در عین حال، به دلیل شرط a + b + c = 1 می توانیم بنویسیم:
(D) a + b < 1
مدل شناسایی توصیف شده در بالا فقط در مواردی که شرایط a + b + c = 1 را برآورده کند قابل استفاده است. این فرضیه مدل کلاسیک Muskingum به این معنی است که حجم سیلاب به سطح مقطع بالادست برابر است با خروجی از پایین دست رسیدن. اگر برآورده نشود، باید از برخی از روشها استفاده کنیم که برای واحد بودن به جمع پارامترها نیاز ندارد. معمولاً در عمل:
a + b + c < 1.
5.2.11. آزمایش و شناسایی خطا
این روش با اختصاص مقادیری برای پارامترها در حوزه امکان سنجی و محاسبه تابع خطا کار می کند. بدیهی است که هرچه تعداد ناشناخته های ما بیشتر باشد، زمان مورد نیاز برای یافتن یک محلول مناسب به اندازه کافی نزدیک به نقطه بهینه بیشتر خواهد بود.
مزیت شناسایی توسط آزمایشات این است که کاربر تمام اندازه اندازه پارامترها و همچنین روند پیشرفت جستجو را کنترل می کند. به این ترتیب، از نظر فیزیکی، از برخی مقادیر ناکافی برای پارامترها جلوگیری می شود.
برای جلوگیری از چنین وضعیتی در مدلهایی که به طور خودکار شناسایی را اجرا می کنند، باید شرایط اضافی مربوط به مرزهای تغییر برای متغیرها یا نسبت آنها را معرفی کنیم. به عنوان مثال، در مورد مدل های آبخوان، تغییرات ناگهانی در انتقال دو عنصر مجاور امکان پذیر نیست.
با افزودن این شرایط تکمیلی، پیچیدگی مدل های کالیبراسیون خودکار ممکن است به طور اغراق آمیزی افزایش یابد. اما در صورت شناسایی توسط آزمایشات، این شرایط لازم نیست زیرا کاربر باید حتی به روشی که مقادیر جدید را برای متغیرها انتخاب می کند، به آنها احترام بگذارد.
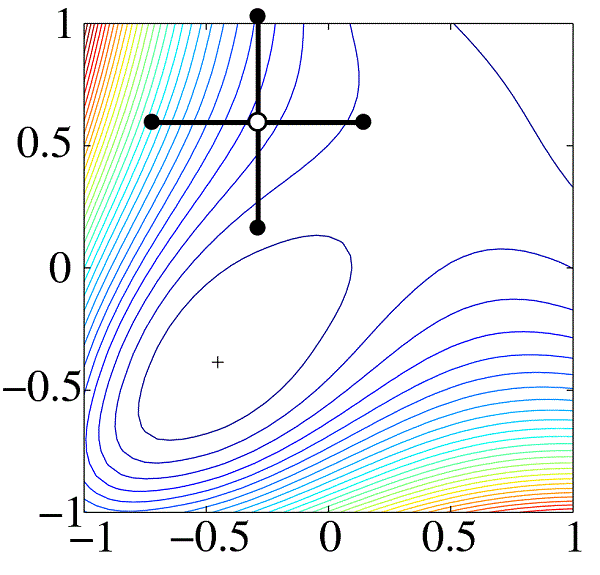
نوع روش "آزمون و خطا"، روش کاوش کامل است که در صورت بروز مشکلات با تعداد کمی از ناشناخته ها (2 = n یا حتی 3 = n) قابل استفاده است. بنابراین، برای n = 2، بعد از اینکه مقادیر تابع f(x1,x2) را در چندین نقطه از یک شبکه مستطیلی با اندازه مش ثابت یا متغیر محاسبه کردیم، می توانیم خطوط تابع را ترسیم کنیم (منحنی های اتصال نقاطی که تابع مقادیر برابر هستند). این امر امکان مشاهده مستقیم منطقه بهینه را فراهم می کند (شکل 14.11).
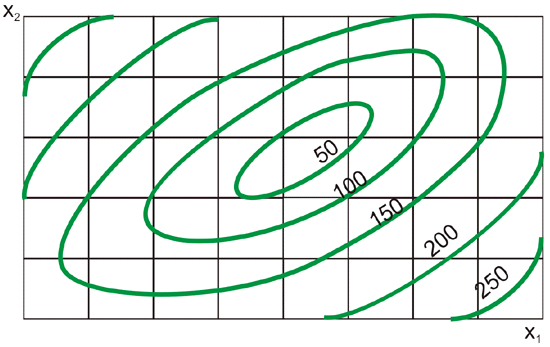
شکل 14.11 - شناسایی بهینه با استفاده از کاوش جامع.
وقتی n = 3 مقادیر ثابت را به یکی از متغیرها اختصاص می دهیم، x3 برای مثال x3 = k1; x3 = k2; ...;x3 = km
برای هر مقدار x3 منحنی مقادیر برابر تابع f(x1,x2,x3 = kj) را ردیابی خواهیم کرد، بنابراین حداقل تعداد تابع f(x) حاصل می شود. با رسم حداقل مقادیر f(x) در برابر x3 می توان مقدار بهینه x3 را پیدا کرد (شکل 15.11):
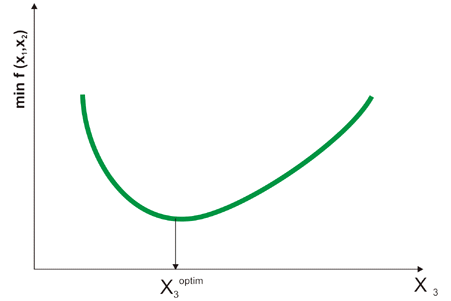
شکل 15.11 شناسایی بهینه برای مسائل 3 بعدی
بعداً، با ترسیم خطوط منحنی φ(x1,x2)، به دنبال تابع دو متغیر φ(x1,x2) = f(x1,x2,x3min) هستیم.
بدیهی است که این روش را نمی توان در توابع بیش از 3 متغیر اعمال کرد. در این حالت مکان سریع بهینه بستگی به تجربه کاربر، شهود وی در مورد پیشرفت فرایند تجزیه و تحلیل و توانایی او در استفاده از اطلاعات کیفی مانند: ترتیب اندازه پارامترها و رابطه بین پدیده مورد مطالعه و سایر موارد دارد. پدیده های متصل در بسیاری از مواقع، نمی توان این اطلاعات را از نظر ریاضی سنجید، و این نیاز به استفاده از روشی از نوع "آزمون و خطا" را، علیرغم سایر روشهای کارآمد بهینه سازی، توضیح می دهد.
در عین حال، با استفاده از این روش به درک بهتری از پدیده مورد مطالعه می رسیم و حتی می توانیم مدل ریاضی را بهبود ببخشیم.
منابع
download the EndNote library for this module
Anderson, G. M., and P. T. Burt. 1990. Hydrological Forecasting. John Willey and Sons Ltd.
Anderson, G. M., and P. T. Burt. 1990. Process Studies in Hillslope Hydrology. John Willey and Sons Ltd.
Austin, P. M., and R. A. Honze. 1972. Analysis of the structure of precipitation patterns in New England. Journal. Appl. Meteorology 11.
Beven, J. K., and D. I. Moore. 1991. Advances Analyses and Distributed Modeling in Hydrology. John Willey and Sons Ltd.
Chow, V. T. 1959. Open channel hydraulics. McGraw-Hill Book Co., New York.
Chow, V. T. 1964. Handbook of Applied Hydrology. McGraw-Hill Book Company.
Chow, V. T., D. Maidment, and L. Mays. 1988. Applied Hydrology. McGraw-Hill Book Company, New York.
Cordery, I., and D. M. Pilgrim. 1984. Time Patterns of Rainfall for Estimating Design Floods on a Frequency Basis. Wat. Sci. Tech. 16:155-165.
Cunge, J. A. 1969. On the subject of a flood propagation method (Muskingum method). J. Hydraulics Research, IAHR 7.
Cunge, J. A., F. M. Holly, and A. Verwey. 1980. Practical aspects of computational river hydraulics. Pitman Publ. Ltd., London.
Diaconu, C. 1988. Space –Time Analysis and probabilities. in Meteorology and Hydrology, Bucharest.
Drobot, R. 1983. Evaluation of the Muskingum model parameters by linear pro-gramming (in Romanian). Hidrotehnica Journal 28.
Drobot, R., and F. Moldoveanu. 1995. Extension of the Muskingum model for n sub-reaches (in Romanian). Buletinul Stiintific al UTCB XXXIX.
Drobot, R., and P. Serban. 1999. Aplicatii de hidrologie si gospodarirea apelor (Application of Hydrology and Water Resources Management). Ed. HGA, Bucuresti, Romania.
Drobot, R., C. Toma, and I. Iorgulescu. 1987. Muskingum model with variable parameters (in Romanian). Hidrotehnica Journal 32.
Dujardin, J. M. 1980. Exemples concrets d'annonce des crues dans des petits bassins versants. La Houille Blanche.
Geiger, W., I. Marsalek, W. I. Rawls, and F. C. Zuidema. 1987. Manual on Drainage in Urbanised Areas Vol. I - Planning and Design Drainage Systems. Studies and Reports in Hydrology No. 43, UNESCO, Paris.
Geiger, W. F. 1990. New Dimensions in Urban Drainage, Osaka.
Geiger, W. F., W. H. Gilbrich, E. E. Herricks, H. W. Hissink, E. Jacobs, J. Marsalek, and S. G. Walwessh. 1994. Integrated Water Resources Management in Urban and Surrounding Areas, Part. 1: Manual. in International Workshop. UNESCO, Gelsenkirchen.
Gloor, R., and M. Walter. 1986. Estimation des débits d'étiage sur des cours d'eau sans mesures directes. Pages 37-100 in Beitrage zur Geologie der Schweitz-Hydrologie. Ecole Polytechnique Fédérale de Lausanne, Lausanne.
Graff, W., Altinakar, M.S. 1996. Ecoulement non permanent et phenomenes de transport. Presse Polytechnique et Universitaires Romandes, Lausanne.
Hartig, J. H., and J. R. Vallentyne. 1989. Use of an Ecosystem Approach to Restore Degrades Areas of Great Lakes. Ambio XVIII:423-428.
Huber, W. C., and R. E. Dickinson. 1988. Storm Water Management Model, Version 4, User's Manual. U. S. Environmental Protection Agency, Athens.
Huff, F. A. 1967. Time distribution of rainfall in heavy storms. Water Resources Research 3.
Jaton, J. F. 1984. Métodes de détermination des debits d’étiage. EPFL, Institut d’Aménagement des Terre et des Eaux, HYDRAM, Lausanne.
Jaton, J. F., A. Musy, and P. Regamey. 1978. Methode de prédétermination de débits de ruisselement basé sur l’état de saturation antérieur du bassin, Rapports du Symposium sur les drainage des routes. OCDE, Paris.
Keifer, J. C., and H. H. Chu. 1957. Synthetic Storm Patterns for Drainage Design. Journal of Hydraulics Division 83.
Llamas, J. 1993. Hydrologie Générale. Principes et applications, 2nd edition. Gaëtan Morin Editeur.
Maidment, D. 1993. Handbook of Hydrology. McGraw-Hill, Inc.
Maksimovic, C. 1993. Measurements of water quantity in urban areas. Technical Report submitted to the Hydrology Commission of WMO (draft).
Maksimovic, C., J. Marsalek, J. Niemczinowicz, M. Bignoles, and E. Woloszyn. 1992. Operational Hydrology in Urban Areas. in Wmo-ninth Session of the Commission for Hydrology.
Maksimovic, C., and M. Radojkovic. 1986. Urban Drainage Catchments, Selected Worldwide Rainfall-Runoff Data from Experimental Catchments. Pergamon Press, Oxford.
Morell, M., B. Thebe, and Y. L'Hote. 1999. Acquisition et construction d'une information hydrologique de base. Ed. HGA, Bucuresti.
Mulvaney, T. J. 1881. On the Use of Self-registering rain and Flood Gages in Making Observations of the Relation of Rainfall and Flood Discharges in a Given Catchment. Proc. Inst. Civil Ireland 4:18-31.
Musy, A. 1998. Hydrologie appliquée. in Cours polycopié d'hydrologie générale, Lausanne, Suisse.
Musy, A. 1998. Hydrologie Appliquée (Applied Hydrologie). Ed. HGA, Bucharest.
Musy, A. 2001. e-drologie. Ecole Polytechnique Fédérale, Lausanne, Suisse.
Nash, J. E. 1957. The form of the instantaneous unit hydrograph. in Proceedings of the IAHS General Assembly of Toronto, Toronto.
Niemczynovicz, J., and P. Dahlblom. 1984. Dynamic properties of rainfall in Lund. Nordic Hydrology 15.
Nix, S. J. 1994. Urban Stormwater Modeling and Simulation. Lewis Publishers, Boca, Raton, Ann, Arbor, London, Tokio.
Platagea, G. 1966. Parametri ai ploilor torentiale utilizati in calculele hidrologice privind scurgerea maxima (Parameters of the design storms used for deriving the design maximum runoff). Studii de hidrologie XVII-ISCH:84-85.
Popa, R. 1997. Elements of River Hydrodynamics (in Romanian). Didactica si Pedagogica, Bucharest.
Popa, R. 1998. Modelarea calitatii apei din rauri. Ed. HGA, Bucuresti.
Remenieras, G. 1960. L'Hydrologie de l'ingenieur. Eyrollles, Paris.
Roche, P. A. 1986. Guide de prevision des crues, Tome 1: Texte principal. Societe Hydrotechnique de France, Paris.
Sauvageot, H. 1982. Radar meteorologie, Teledetection active de l'atmosphere. Eyrolles, Paris.
Schaffranek, R. W., R. A. Baltzer, and D. E. Goldberg. 1981. A model for simulation of flow in singular and interconnected channels. Rapport TWI7-C3, US Geological Survey.
Serban, P., and G. Balut. 1975. In problema analizei distributiei in timp a ploilor (In the problem of the time distribution of the rainstorms). Studii de hidrologie XLIV-IMH.
Serban, P., V. A. Stanescu, and P. Roman. 1989. Dynamic Hydrology (in Romanian). Editura Tehnica.
Sevruk, B. 1982. Methods of correction for systematic errors in point precipitation measurements for operational use. WMO Operational Hydrology Report, No. 21.
Siccardi, F. 1993. Urban Hydrology. in The TEMPUS-High Post-universitary Training Courses For Hydrology and Water Management, Bucharest.
Singh, P. V. 1992. Elementary Hydrology. Prentice Hall.
Stanescu, V. 1986. Forecasting Relations of the Mean Monthly Discharges in the Summer-Autumn Period (In Romanian). Hidrotehnica Journal 29.
Stanescu, V. A. 1995. Hidrologie urbana (Urban Hydrology). Editura Didactica si Pedagogica, Bucharest.
Stankowski, S. J. 1974. Magnitude and Frequency of Floods in New Jersey with Effect of Urbanization. Special Report 38, U. S. Geological Survey, Water Resources Division, Trenton, NJ.
Strelkoff, T. 1970. Numerical solution of Saint-Venant equations. J. Hydraulics Div. 96.
Vladimirescu, I. 1984. Engineering Hydrology (In Romanian). Editura Tehnica, Bucuresti.
Ward, R. C., and M. Robinson. 1990. Principles of Hydrology. McGraw-Hill International Editions.
WMO. 1983. Guide to hydrological practices, 5 edition. OMM, Geneva.
WMO. 1983. Guide to meterological instruments and methods of observation, 5 edition. OMM, Geneva.
Woolisher, D., and H. C. Schwalen. 1959. Frequency Relations for Thunderstorm Rainfall in Southern Arizona. Technical Paper, Univ. Arizona. Agr. Depart.
Zuidema, F. C. 1982. Aspects of Water Resources Planning and Management in the Urbanization Process. Pages 297-340 in P. Laconte and Y. Y. Haimes, editors. Water Resources and Land Use Planning: A Systemic Approach. Martimus Nijhoff Publishers, The Hague.


مدیر سایت: بهزاد سرهادی کارشناس ارشد مهندسی آب
شناسه تلگرام مدیر سایت: SubBasin@
نشانی ایمیل: behzadsarhadi@gmail.com
(سوالات تخصصی را در گروه تلگرام ارسال کنید)
_______________________________________________________
پروژه تخصصی در لینکدین









 در منابع آب
در منابع آب





































نظرات (۰)